题目内容
设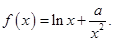
(1)求f(x)的单调区间;
(2)求f(x)的零点个数.
(1)见解析;(2)见解析.
解析试题分析:(1)先由对数函数的定义求得函数的定义域,然后对函数求导,对 的取值进行分类讨论,根据函数的单调性与导数的关系求得每种情况下的函数的单调区间;(2) 对
的取值进行分类讨论,根据函数的单调性与导数的关系求得每种情况下的函数的单调区间;(2) 对 的取值进行分类讨论,当
的取值进行分类讨论,当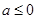 时分
时分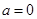 和
和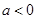 两种情况,由
两种情况,由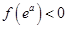 ,
, 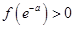 ,结合零点存在性定理可知
,结合零点存在性定理可知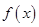 在
在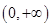 上有一个零点;当
上有一个零点;当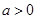 时,根据函数的单调性求得函数的极小值
时,根据函数的单调性求得函数的极小值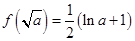 ,对极小值与0的关系分三种情况进行分类讨论,结合零点存在性定理求得每种情况下的函数的零点个数.
,对极小值与0的关系分三种情况进行分类讨论,结合零点存在性定理求得每种情况下的函数的零点个数.
试题解析:(1) 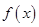 的定义域是
的定义域是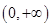 , 1分
, 1分
∵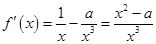 , 2分
, 2分
当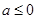 时,
时,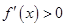 ,
,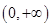 是
是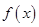 的增区间, 3分
的增区间, 3分
当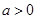 时,令
时,令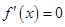 ,
,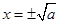 ,(负值舍去)
,(负值舍去)
当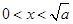 时,
时,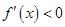 ;当
;当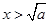 时,
时,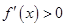 5分
5分
所以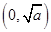 是
是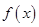 的减区间,
的减区间,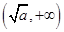 是
是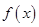 的增区间. 6分
的增区间. 6分
综合:当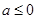 时,
时,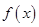 的增区间是
的增区间是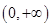 ;
;
当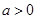 时,
时,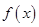 的减区间是
的减区间是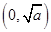 ,
,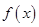 的增区间是
的增区间是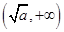 . 7分
. 7分
(2)由(1)知道当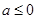 时,
时,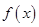 在
在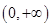 上是增函数,当
上是增函数,当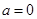 时有零点
时有零点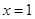 , 8分
, 8分
当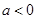 时,
时,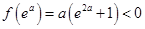 ,
, 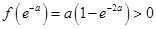 , .9分
, .9分
(或当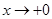 时,
时,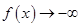 ;当
;当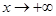 时,
时,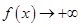 ),
),
所以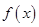 在
在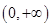 上有一个零点, 10分
上有一个零点, 10分
当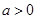 时,由(1)知,
时,由(1)知,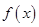 在
在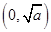 上是减函数,
上是减函数,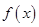 在
在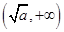 上是增函数,所以当
上是增函数,所以当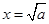 是,
是,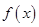 有极小值,其最小值为
有极小值,其最小值为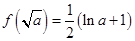 . 11分
. 11分
当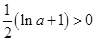 ,即
,即 时,
时,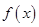 无零点,
无零点,
当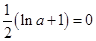 ,即
,即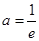 时,
时,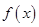 有一个零点,
有一个零点,
当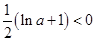 ,即
,即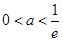 时,
时,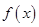 有2个零点. 13分
有2个零点. 13分
综合:当 时,
时,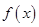

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,试利用基本初等函数的图象,判断f(x)有几个零点,并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1).
,试利用基本初等函数的图象,判断f(x)有几个零点,并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1). 中,已知椭圆
中,已知椭圆 :
: 的离心率
的离心率 ,且椭圆C上一点
,且椭圆C上一点 到点Q
到点Q 的距离最大值为4,过点
的距离最大值为4,过点 的直线交椭圆
的直线交椭圆
 (O为坐标原点),当
(O为坐标原点),当 时,求实数
时,求实数 的取值范围.
的取值范围. 的解集为M.
的解集为M. ,求实数
,求实数 的取值范围;
的取值范围; ,求实数
,求实数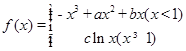 的图像在点
的图像在点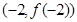 处的切线方程为
处的切线方程为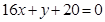 .
.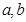 的值;
的值; 在区间
在区间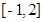 上的最大值;
上的最大值;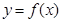 上存在两点
上存在两点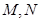 使得
使得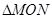 是以坐标原点
是以坐标原点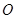 为直角顶点的直角三角形,且斜边
为直角顶点的直角三角形,且斜边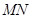 的中点在
的中点在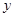 轴上,求实数
轴上,求实数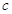 的取值范围.
的取值范围. 图象上一点
图象上一点 处的切线方程为
处的切线方程为 .
. 的值;
的值; 在
在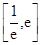 内有两个不等实根,求
内有两个不等实根,求 的取值范围(其中
的取值范围(其中 为自然对数的底数);(3)令
为自然对数的底数);(3)令 ,若
,若 的图象与
的图象与 轴交于
轴交于 (其中
(其中 ),
), 的中点为
的中点为 ,求证:
,求证: 处的导数
处的导数
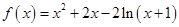 .
. 的单调区间;
的单调区间; 时,是否存在整数
时,是否存在整数 ,使不等式
,使不等式 恒成立?若存在,求整数
恒成立?若存在,求整数 的方程
的方程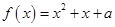 在
在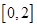 上恰有两个相异实根,求实数
上恰有两个相异实根,求实数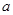 的取值范围.
的取值范围.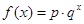 ;②
;②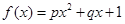 ;③
;③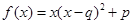 .(以上三式中
.(以上三式中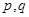 均为常数,且
均为常数,且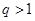 )
)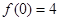 ,
,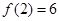 ,求出所选函数
,求出所选函数 的解析式(注:函数定义域是
的解析式(注:函数定义域是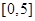 .其中
.其中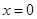 表示8月1日,
表示8月1日,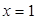 表示9月1日,…,以此类推);
表示9月1日,…,以此类推);