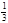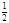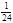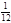题目内容
(本小题满分12分)从2003年开始,我国就通过实施高校自主招生探索人才选拔制度改革,允许部分高校拿出一定比例的招生名额,选拔那些有特殊才能的学生。某学生参加一个高校的自主招生考试,考试分笔试和面试两个环节,笔试有A、B两个题目,该学生答对A、B两题的概率分别为 、
、 ,两题全部答对方可进入面试。面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为
,两题全部答对方可进入面试。面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为 ,至少答对一题即可被录取。(假设每个环节的每个问题回答正确与否是相对独立的)
,至少答对一题即可被录取。(假设每个环节的每个问题回答正确与否是相对独立的)
(I)求该学生被学校录取的概率;
(II)设该学生答对题目的个数为ξ,求ξ的分布列和数学期望。
【答案】
解:设该学生答对A、B、甲、乙各题分别为事件A、B、C、D,
则P(A)=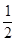 ,P(B)=
,P(B)=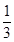 ,P(C)=P(D)=
,P(C)=P(D)=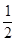 。 (3分)
。 (3分)
(1)所求事件的概率为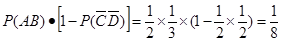 。 (5分)
。 (5分)
(2)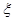 的所有可能取值为0,1,2,3,4,
的所有可能取值为0,1,2,3,4,
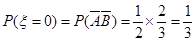 , (6分)
, (6分)
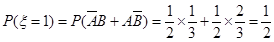 , (7分)
, (7分)
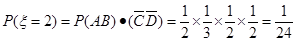 , (8分)
, (8分)
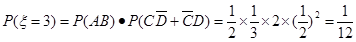 , (9分)
, (9分)
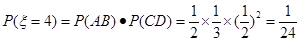 ,
(10分)
,
(10分)
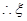 的分布列为
的分布列为
|
|
0 |
1 |
2 |
3 |
4 |
|
P |
|
|
|
|
|
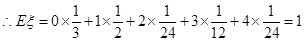 。
(12分)
。
(12分)
【解析】略

练习册系列答案
相关题目