题目内容
4．
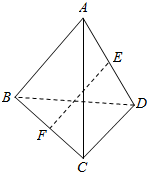已知空间四边形ABCD，F为BC的中点，E为AD的中点，若$\overrightarrow{EF}$=λ（$\overrightarrow{AB}$+$\overrightarrow{DC}$），则λ=（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | 1 | D． | $\frac{1}{4}$ |
分析 取BD中点G，由已知得$\overrightarrow{EG}$=$\frac{1}{2}$$\overrightarrow{AB}$，$\overrightarrow{GF}=\frac{1}{2}\overrightarrow{DC}$，由此能求出实数λ．
解答 
解：如图，取BD中点G，
∵G为BD的中点，F为BC的中点，E为AD的中点，
∴EG∥AB，GF∥DC，
∴$\overrightarrow{EG}$=$\frac{1}{2}$$\overrightarrow{AB}$，$\overrightarrow{GF}=\frac{1}{2}\overrightarrow{DC}$，
∴$\overrightarrow{EF}$=$\overrightarrow{EG}+\overrightarrow{GF}$=$\frac{1}{2}（\overrightarrow{AB}+\overrightarrow{DC}）$，
∵$\overrightarrow{EF}$=λ（$\overrightarrow{AB}$+$\overrightarrow{DC}$），∴λ=$\frac{1}{2}$．
故选：A．
点评 本题考查实数值的求法，是基础题，解题时要认真审题，注意数形结合思想和向量数量加法法则的合理运用．
练习册系列答案
53随堂测系列答案
相关题目
12．函数f（x）=x2-2x-3的值域是（ ）
| A． | [-4，+∞） | B． | （$\frac{5}{4}$，+∞） | C． | （-∞，-4] | D． | （-∞，$\frac{5}{4}$） |
9．已知等差数列{an}的前n项和是Sn，若S30=13S10，S10+S30=140，则S20的值是（ ）
| A． | 60 | B． | 70 | C． | $\frac{170}{3}$ | D． | $\frac{160}{3}$ |
16．已知α终边上的一点P坐标是（sin2，-cos2），则α的一个弧度数为（ ）
| A． | π+2 | B． | $\frac{π}{2}$+2 | C． | $\frac{3π}{2}$-2 | D． | 2-$\frac{π}{2}$ |
13．函数y=$\frac{1}{1+\frac{1}{x}}$的定义域是（ ）
| A． | {x|x∈R，x≠0} | B． | {x|x∈R，x≠1} | C． | {x|x∈R，x≠0，x≠1} | D． | {x|x∈R，x≠0，x≠-1} |