题目内容
(A)若不等式|x+1|-|x-4|≥a+
,对任意的x∈R恒成立,则实数a的取值范围是
(B)已知直线l:
(t为参数),圆C:ρ=2
cos(θ-
)(极轴与x轴的非负半轴重合,且单位长度相同),若直线l被圆C截得弦长为2,则a=
| 4 |
| a |
(-∞,4]∪[-1,0)
(-∞,4]∪[-1,0)
(B)已知直线l:
|
| 2 |
| π |
| 4 |
5±
| 5 |
5±
.| 5 |
分析:(A)由于|x+1|-|x-4|的最小值为5,可得-5≥a+
,即
≤0,由此求得实数a的取值范围.
(B)把直线l的参数方程化为普通方程,把圆的极坐标方程化为直角坐标方程,利用直线和圆的位置关系以及弦长2
求出a的值.
| 4 |
| a |
| (a+1)(a+4) |
| a |
(B)把直线l的参数方程化为普通方程,把圆的极坐标方程化为直角坐标方程,利用直线和圆的位置关系以及弦长2
求出a的值.
解答:解:(A)由于|x+1|-|x-4|表示数轴上的x对应点到-1对应点的距离减去它到4对应点的距离,其最小值等于-5,
由题意可得-5≥a+
,即
≤0,解得a≤-4或-1≤a<0,
故答案为(-∞,4]∪[-1,0).
(B)直线l:
(t为参数),即 x+2y-a+2=0.圆C:ρ=2
cos(θ-
),
即 ρ2=2
ρcos(θ-
)=2ρcosθ+2ρsinθ.
故圆C:(x-1)2+(y-1)2=2,表示以(1,1)为圆心,以
为半径的圆.
圆心到直线的距离d=
=
,
再由弦长2=2
=2
,解得a=5±
,
故答案为 5±
.
由题意可得-5≥a+
| 4 |
| a |
| (a+1)(a+4) |
| a |
故答案为(-∞,4]∪[-1,0).
(B)直线l:
|
| 2 |
| π |
| 4 |
即 ρ2=2
| 2 |
| π |
| 4 |
故圆C:(x-1)2+(y-1)2=2,表示以(1,1)为圆心,以
| 2 |
圆心到直线的距离d=
| |1+2-a+2| | ||
|
| |a-5| | ||
|
再由弦长2=2
| r2-d2 |
2-
|
| 5 |
故答案为 5±
| 5 |
点评:本题主要考查绝对值不等式的解法,分式不等式的解法,直线和圆的位置关系,把参数方程化为普通方程的方法,
把极坐标方程化为直角坐标方程的方法,属于中档题.
把极坐标方程化为直角坐标方程的方法,属于中档题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
 A.若不等式|x-1|+|x-m|<2m的解集为∅,则m的取值范围为
A.若不等式|x-1|+|x-m|<2m的解集为∅,则m的取值范围为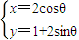 (θ为参数)所截得的弦长为 .
(θ为参数)所截得的弦长为 .