题目内容
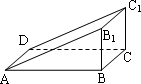
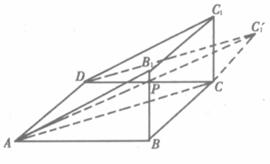
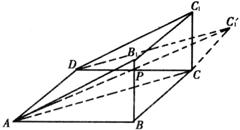
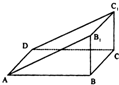 如图直三棱柱ABB1-DCC1中,∠ABB1=90°,AB=4,BC=2,CC1=1,DC上有一动点P,则△APC1周长的最小值是
如图直三棱柱ABB1-DCC1中,∠ABB1=90°,AB=4,BC=2,CC1=1,DC上有一动点P,则△APC1周长的最小值是分析:不妨令CP=a,则DP=4-a,分别在直角三角形ADC中求AP,在直角三角形C1PC求出C1P,在直角三角形C1CA求出C1A,然后相交求周长.将周长表示为参数a的函数,由于a∈[0,4],在这个区间上求出周长的最小值即可.
解答:解:DC上有一动点P,令CP=a,则DP=4-a,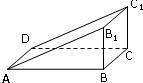
由于直三棱柱ABB1-DCC1中,∠ABB1=90°,AB=4,BC=2,CC1=1,
∴周长S=AP+C1P+C1A=
+
+
=
+
+
=
+
+
=
+
+
其中是
+
可以看作平面直角坐标系中(a,0)与两点(4,-2)以及(0,1)两点距离和的最小值,由图形中点(a,0)恰好是过两点(4,-2)与(0,1)的直线与x轴的交点时,上式的值最小.
由两点式知过两点(4,-2)与(0,1)的直线的方程是3x+4y-4=0,其与x轴的交点是(
,0),
即当a=
时,
+
的最小值为两点(4,-2)与(0,1)的距离,其值为
=5,故周长为5+
故答案为5+

由于直三棱柱ABB1-DCC1中,∠ABB1=90°,AB=4,BC=2,CC1=1,
∴周长S=AP+C1P+C1A=
| 4+(4-a)2 |
| 1+a2 |
| 1+|AC|2 |
=
| 4+(4-a)2 |
| 1+a2 |
| 1+22+42 |
=
| 4+(4-a)2 |
| 1+a2 |
| 21 |
=
| [0-(-2)]2+(a-4)2 |
| (0-1) 2+(a-0)2 |
| 21 |
其中是
| [0-(-2)]2+(a-4)2 |
| (0-1) 2+(a-0)2 |
由两点式知过两点(4,-2)与(0,1)的直线的方程是3x+4y-4=0,其与x轴的交点是(
| 4 |
| 3 |
即当a=
| 4 |
| 3 |
| [0-(-2)]2+(a-4)2 |
| (0-1) 2+(a-0)2 |
| (4-0)2+ (-2-1)2 |
| 21 |
故答案为5+
| 21 |
点评:本题考点是点、线、面之间的距离,考查用勾股定理在直角三角形中求两点间的距离,解答本题的关键是找到所求线段存在的直角三角形,由于本题是一个直三棱柱且其两个侧面垂直,这为找出各求各边所在的直角三角形带来了方便,此做法空间想象能力要求较高,解答本题也可以用空间向量法,请做题时比较一下两种方法在求最值方面的异同.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
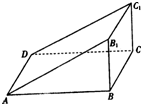 如图,直三棱柱ABB1-DCC1中,∠ABB1=90°,AB=4,BC=2,CC1=1,DC上有一动点P,则△APC1周长的最小值为( )
如图,直三棱柱ABB1-DCC1中,∠ABB1=90°,AB=4,BC=2,CC1=1,DC上有一动点P,则△APC1周长的最小值为( )