题目内容
在△ABC中，AC=2，BC=2，∠ACB=120°，若△ABC绕直线BC旋转一周，则所形成的几何体的表面积是（ ）
分析：△ABC绕直线BC旋转一周，所形成的几何体一个大圆锥去掉一个小圆锥，几何体的表面积是两个圆锥表面积的和．
解答：解：△ABC绕直线BC旋转一周，所形成的几何体一个大圆锥去掉一个小圆锥，
因为AC=2，BC=2，∠ACB=120°，所以OA=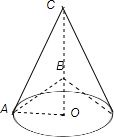
，AB=2
所以所形成的几何体的表面积是π×
×(2+2
)=(6+2
)π
故选A．
因为AC=2，BC=2，∠ACB=120°，所以OA=
| 3 |
| 3 |
所以所形成的几何体的表面积是π×
| 3 |
| 3 |
| 3 |
故选A．
点评：本题考查旋转体的表面积，确定旋转体的形状是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
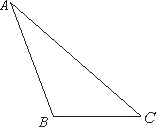如图，在△ABC中，AC=2，BC=1，
如图，在△ABC中，AC=BC，AB=2，O为AB的中点，沿OC将△AOC折起到△A′OC的位置，使得直线A′B与平面ABC成30°角．