题目内容
如图,点An(xn,yn)是曲线y2=2x(y≥0)上的点,点Bn(an,0)是x轴上的点,△Bn-1AnBn是以An为直角顶点的等腰直角三角形,其中n=1,2,3,…,B0为坐标原点.
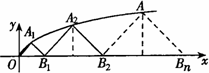
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列bn=2n-1,求最小正整数m,使得对任意的n∈N*,当n>m时,an<bn成立.
答案:
解析:
解析:
|
解:(Ⅰ)∵点 ∵△ ∵ 由 ∴ ∴ (Ⅱ)∵当 可以猜想,当 设 当 ∵ 综上, |

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
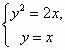 可以解得
可以解得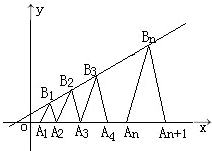 函数y=f(x)是定义在R上的偶函数,且f(-1+x)=f(-1-x),当x∈[-2,-1]时,f(x)=t(x+2)3-t(x+2)(t∈R),记函数y=f(x)的图象在(
函数y=f(x)是定义在R上的偶函数,且f(-1+x)=f(-1-x),当x∈[-2,-1]时,f(x)=t(x+2)3-t(x+2)(t∈R),记函数y=f(x)的图象在(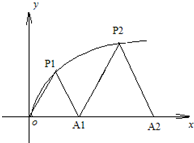 如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn) 是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).
如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn) 是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点). (2006•南京二模)如图,已知曲线C:
(2006•南京二模)如图,已知曲线C: 如图,已知曲线C:
如图,已知曲线C: