题目内容
过点O(0,0)的圆C与直线y=2x-8相切于点P(4,0).
(1)求圆C的方程;
(2)已知点B的坐标为(0,2),设P,Q分别是直线l:x+y+2=0和圆C上的动点,求|PB|+|PQ|的最小值.
(1)求圆C的方程;
(2)已知点B的坐标为(0,2),设P,Q分别是直线l:x+y+2=0和圆C上的动点,求|PB|+|PQ|的最小值.
分析:(1)求出圆的圆心坐标,求出圆的半径,即可求圆C的方程;
(2)求出点B关于直线l:x+y+2=0的对称点的坐标A,转化|PB|+|PQ|为|PA|+|PQ|,然后求解它的最小值.
(2)求出点B关于直线l:x+y+2=0的对称点的坐标A,转化|PB|+|PQ|为|PA|+|PQ|,然后求解它的最小值.
解答: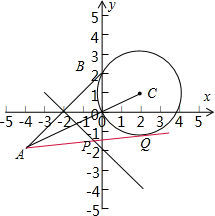 解.(1)由已知得圆C经过点P(4,0),
解.(1)由已知得圆C经过点P(4,0),
圆心在与y=2x-8垂直的直线y=-
x+2上,
它又在线段OP的中垂线x=2上,
所以
,
求得圆心C(2,1),半径为
,
所以圆C的方程为(x-2)2+(y-1)2=5…(4分)
(2)求得点B(0,2)关于直线l:x+y+2=0的对称点A(-4,-2),
所以|PB|+|PQ|
=|PA|+|PQ|≥|AQ|≥|AC|-
=
=3
-
=2
,
所以|PB|+|PQ|的最小值是2
.…(9分)
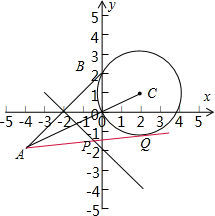 解.(1)由已知得圆C经过点P(4,0),
解.(1)由已知得圆C经过点P(4,0),圆心在与y=2x-8垂直的直线y=-
| 1 |
| 2 |
它又在线段OP的中垂线x=2上,
所以
|
求得圆心C(2,1),半径为
| 5 |
所以圆C的方程为(x-2)2+(y-1)2=5…(4分)
(2)求得点B(0,2)关于直线l:x+y+2=0的对称点A(-4,-2),
所以|PB|+|PQ|
=|PA|+|PQ|≥|AQ|≥|AC|-
| 5 |
| (2+4)2+(1+2)2 |
| 5 |
| 5 |
| 5 |
所以|PB|+|PQ|的最小值是2
| 5 |
点评:本题考查直线与圆的位置关系,对称知识的应用,考查计算能力以及转化思想的应用.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目