题目内容
14．
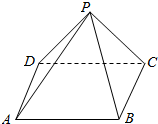已知正四面棱锥P-ABCD的侧棱长为2$\sqrt{3}$，侧面等腰三角形的顶角为30°，则从A点出发环绕面一周后回到A点的最短路程为（ ）| A． | 2$\sqrt{6}$ | B． | 2$\sqrt{3}$ | C． | $\sqrt{6}$ | D． | 6 |
分析 用空间思维将此正四棱锥的侧面展开，得到一个由四个全等的顶角为30°的等腰三角形组成的图形，所求的路径，是一个以2$\sqrt{3}$为腰长，120°为顶角的三角形的底边，由余弦定理可得最短路程．
解答 解：用空间思维将此正四棱锥的侧面展开，得到一个由四个全等的顶角为30°的等腰三角形组成的图形，
所求的路径，是一个以2$\sqrt{3}$a为腰长，120°为顶角的三角形的底边，
由余弦定理可得最短路程等于$\sqrt{12+12-2•2\sqrt{3}•2\sqrt{3}•（-\frac{1}{2}）}$=6．
故选：D．
点评 本题考查正四棱锥的侧面展开图，考查余弦定理，考查学生的计算能力，正确运用正四棱锥的侧面展开图是关键．
练习册系列答案
相关题目
15．C${\;}_{4}^{1}$+C${\;}_{5}^{2}$+…+C${\;}_{20}^{17}$等于（ ）
| A． | C${\;}_{21}^{17}$ | B． | C${\;}_{21}^{17}$-1 | C． | C${\;}_{21}^{18}$-1 | D． | C${\;}_{21}^{18}$ |
5．当x→0时，下列四个无穷小阶数最高的是（ ）
| A． | e${\;}^{{x}^{4}-{x}^{3}}$-1 | B． | cosx2-1 | C． | $\sqrt{1+{x}^{2}}$-1 | D． | tanx-sinx |
2．如图所示，在棱长为1的正方体ABCD-A1B1C1D1中，P是A1B上一动点，则AP+D1P的最小值为（ ）
| A． | 2 | B． | $\frac{{\sqrt{6}+\sqrt{2}}}{2}$ | C． | $2+\sqrt{2}$ | D． | $\sqrt{2+\sqrt{2}}$ |
9．
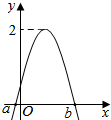如图是函数$f（x）=Asin（2x+ϕ），（A＞0，|ϕ|≤\frac{π}{2}）$图象的一部分，对不同的x1，x2∈[a，b]，若f（x1）=f（x2），有$f（{x_1}+{x_2}）=\sqrt{2}$，则（ ）
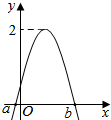如图是函数$f（x）=Asin（2x+ϕ），（A＞0，|ϕ|≤\frac{π}{2}）$图象的一部分，对不同的x1，x2∈[a，b]，若f（x1）=f（x2），有$f（{x_1}+{x_2}）=\sqrt{2}$，则（ ）| A． | f（x）在$（-\frac{3π}{8}，\frac{π}{8}）$上是增函数 | B． | f（x）在$（-\frac{3π}{8}，\frac{π}{8}）$上是减函数 | ||
| C． | f（x）在$（-\frac{5π}{12}，\frac{π}{12}）$上是增函数 | D． | f（x）在$（-\frac{5π}{12}，\frac{π}{12}）$上是减函数 |
19．已知函数f（x）满足f（x+1）=f（x-1），且f（x）是偶函数，当x∈[0，1]时，f（x）=2x-1，若在区间[-1，3]内，函数g（x）=f（x）-kx-k有4个零点，则实数k的取值范围是（ ）
| A． | $[\frac{1}{4}，\frac{1}{3}）$ | B． | $（0，\frac{1}{2}）$ | C． | $（0，\frac{1}{4}]$ | D． | $（\frac{1}{3}，\frac{1}{2}）$ |