题目内容
如图.在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB,点M是SD上的点,AM与BC所成的角为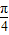 ,
,AN⊥SC,垂足为点N.
(I)求证:SB∥平面ACM;
( II)求直线AC与平面SDC所成的角;
(Ⅲ)求二面角N-AM-C的大小.
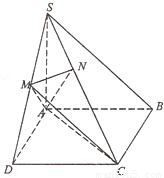
【答案】分析:(I)由题意连接BD交AC于E,连接ME,根据ME是三角形DSB的中位线进行证明;
(II)由题可得,CD⊥平面SAD,直线AC与平面SDC所成的角为∠ACM,然后在Rt△AMC中进行求解;
(Ⅲ)因为AM⊥平面SCD,所以∠NMC为二面角N-AM-C的一个平面角,然后在直角三角形中求其余弦值,从而求解.
解答: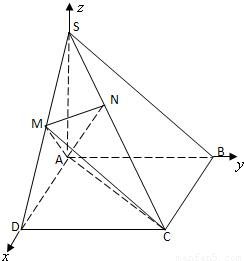 解法一:依题意有AD∥BC,所以
解法一:依题意有AD∥BC,所以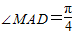
所以点M是SD的中点,且AM⊥SD(3分)
(Ⅰ)证明:连接BD交AC于E,连接ME(4分)
∵ABCD是正方形,
∴E是BD的中点∵M是SD的中点,
∴ME是△DSB的中位线
∴ME∥SB(5分)
又∵ME?平面ACM,SB?平面ACM,
∴SB∥平面ACM. (6分)
(Ⅱ)由题可得,CD⊥平面SAD,所以有CD⊥AM,又SD⊥AM
∴AM⊥平面SCD,
∴∠ACM为直线AC与平面SDC所成的角(8分)
在Rt△AMC中,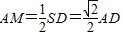 ,
,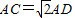
∴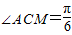 ,即直线AC于平面SDC所成的角为
,即直线AC于平面SDC所成的角为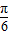 (9分)
(9分)
(Ⅲ)∵AM⊥平面SCD
∴∠NMC为二面角N-AM-C的一个平面角(10分)
且AM⊥SC,又AN⊥SC
∴SC⊥平面AMN∴SC⊥MN.
在Rt△MNC中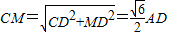 ,
,
∵Rt△SNM∽Rt△SDC
∴
∴
∴二面角N-AM-C的大小为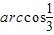 (12分)
(12分)
解法二:依题意有AD∥BC,所以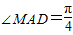
所以点M是SD的中点,且AM⊥SD
如图,以A为坐标原点,建立空间直角坐标系O-xyz,
由SA=AB故设AB=AD=AS=1则A(0,0,0),B(0,1,0),C(1,1,0),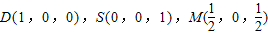 (3分)
(3分)
(Ⅰ)连接BD交AC于E,则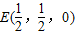
∵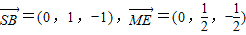
∴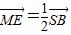
∴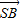 ∥
∥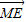
∴SB∥平面ACM(6分)
(Ⅱ)由题可得,CD⊥平面SAD,所以有CD⊥AM
又SD⊥AM
∴AM⊥平面SCD
∴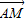 为平面SCD的一个法向量
为平面SCD的一个法向量
∴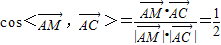
∴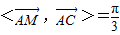
∴直线AC于平面SDC所成的角为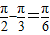 (9分)
(9分)
(Ⅲ)∵AM⊥平面SCD
∴AM⊥SC,又AN⊥SC
∴SC⊥平面AMN
∴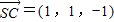 为平面AMN的一个法向量.
为平面AMN的一个法向量.
设平面AMC的一个法向量为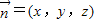 ,则
,则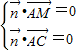 即
即 ,
,
令x=1,则z=y=-1即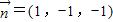
∴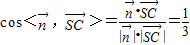
∴二面角N-AM-C的大小为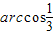 (12分)
(12分)
点评:此题是道综合性比较强的题,考查空间直线与平面平行的判断及二面角的求法,构造直角三角形是解题的关键,此类题型是高考常出的,同学们要注意两种方法的区别和联系.
(II)由题可得,CD⊥平面SAD,直线AC与平面SDC所成的角为∠ACM,然后在Rt△AMC中进行求解;
(Ⅲ)因为AM⊥平面SCD,所以∠NMC为二面角N-AM-C的一个平面角,然后在直角三角形中求其余弦值,从而求解.
解答:
 解法一:依题意有AD∥BC,所以
解法一:依题意有AD∥BC,所以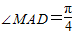
所以点M是SD的中点,且AM⊥SD(3分)
(Ⅰ)证明:连接BD交AC于E,连接ME(4分)
∵ABCD是正方形,
∴E是BD的中点∵M是SD的中点,
∴ME是△DSB的中位线
∴ME∥SB(5分)
又∵ME?平面ACM,SB?平面ACM,
∴SB∥平面ACM. (6分)
(Ⅱ)由题可得,CD⊥平面SAD,所以有CD⊥AM,又SD⊥AM
∴AM⊥平面SCD,
∴∠ACM为直线AC与平面SDC所成的角(8分)
在Rt△AMC中,
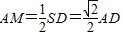 ,
,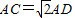
∴
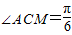 ,即直线AC于平面SDC所成的角为
,即直线AC于平面SDC所成的角为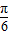 (9分)
(9分)(Ⅲ)∵AM⊥平面SCD
∴∠NMC为二面角N-AM-C的一个平面角(10分)
且AM⊥SC,又AN⊥SC
∴SC⊥平面AMN∴SC⊥MN.
在Rt△MNC中
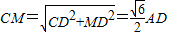 ,
,∵Rt△SNM∽Rt△SDC
∴

∴

∴二面角N-AM-C的大小为
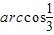 (12分)
(12分)解法二:依题意有AD∥BC,所以
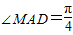
所以点M是SD的中点,且AM⊥SD
如图,以A为坐标原点,建立空间直角坐标系O-xyz,
由SA=AB故设AB=AD=AS=1则A(0,0,0),B(0,1,0),C(1,1,0),
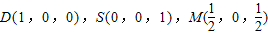 (3分)
(3分)(Ⅰ)连接BD交AC于E,则
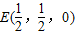
∵
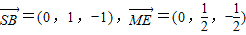
∴
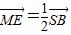
∴
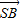 ∥
∥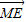
∴SB∥平面ACM(6分)
(Ⅱ)由题可得,CD⊥平面SAD,所以有CD⊥AM
又SD⊥AM
∴AM⊥平面SCD
∴
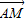 为平面SCD的一个法向量
为平面SCD的一个法向量∴
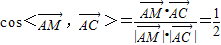
∴
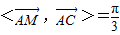
∴直线AC于平面SDC所成的角为
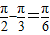 (9分)
(9分)(Ⅲ)∵AM⊥平面SCD
∴AM⊥SC,又AN⊥SC
∴SC⊥平面AMN
∴
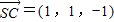 为平面AMN的一个法向量.
为平面AMN的一个法向量.设平面AMC的一个法向量为
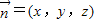 ,则
,则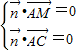 即
即 ,
,令x=1,则z=y=-1即
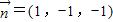
∴
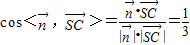
∴二面角N-AM-C的大小为
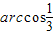 (12分)
(12分)点评:此题是道综合性比较强的题,考查空间直线与平面平行的判断及二面角的求法,构造直角三角形是解题的关键,此类题型是高考常出的,同学们要注意两种方法的区别和联系.

练习册系列答案
相关题目
 如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE=
如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE= 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点 如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=
如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,SA=AB=AD= 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点. 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.底面ABCD为矩形,
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.底面ABCD为矩形,