题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点 在椭圆上.
在椭圆上.
(![]() )求椭圆
)求椭圆![]() 的方程.
的方程.
(![]() )设动直线
)设动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,判断是否存在以原点
有且仅有一个公共点,判断是否存在以原点![]() 为圆心的圆,满足此圆与
为圆心的圆,满足此圆与![]() 相交于两点
相交于两点![]() ,
, ![]() (两点均不在坐标轴上),且使得直线
(两点均不在坐标轴上),且使得直线![]() 、
、![]() 的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
【答案】(1) 椭圆方程为![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(I)借助题设条件建立方程组求解;(II)借助题设运用直线与椭圆的位置关系推证和探求.
试题解析:
(I)由题意得: ![]() ,
, ![]() ,
,
又点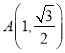 在椭圆
在椭圆![]() 上,∴
上,∴![]() ,解得
,解得![]() ,
, ![]() ,
, ![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .………………5分
.………………5分
(II)存在符合条件的圆,且此圆的方程为![]() .
.
证明如下:假设存在符合条件的圆,并设此圆的方程为![]() .
.
当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为
的方程为![]() .
.
由方程组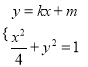 得
得![]() .
.
∵直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,
有且仅有一个公共点,
∴![]() ,即
,即![]() .
.
由方程组![]() 得
得![]() ,
,
则![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,
设直线![]() 的斜率分别为
的斜率分别为![]() ,
,
∴![]()
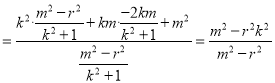 ,将
,将![]() 代入上式,
代入上式,
得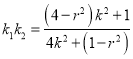 .
.
要使得![]() 为定值,则
为定值,则![]() ,即
,即![]() ,代入
,代入![]() 验证知符合题意.
验证知符合题意.
∴当圆的方程为![]() 时,圆与
时,圆与![]() 的交点
的交点![]() 满足
满足![]() 为定值
为定值![]() .
.
当直线![]() 的斜率不存在时,由题意知
的斜率不存在时,由题意知![]() 的方程为
的方程为![]() .
.
此时,圆![]() 与
与![]() 的交点
的交点![]() 也满足
也满足![]() .
.
综上,当圆的方程为![]() 时,
时,
圆与![]() 的交点
的交点![]() 满足直线
满足直线![]() 的斜率之积为定值
的斜率之积为定值![]() .……………………12分
.……………………12分

练习册系列答案
相关题目