题目内容
已知函数 。
。
(1)当 时,求函数
时,求函数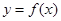 的单调区间;
的单调区间;
(2)求证:当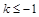 时,对所有的
时,对所有的 都有
都有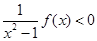 成立.
成立.
(1)当 时,
时,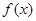 的减区间为
的减区间为 ,无增区间;
,无增区间;
(2)通过求导数, ,
,
由 ,得到
,得到
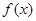 在
在 均为单调减函数.
均为单调减函数.
分 和
和 讨论得证.
讨论得证.
解析试题分析:(1)根据
确定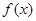 的减区间为
的减区间为 ,无增区间;
,无增区间;
(2)通过求导数, ,
,
由 ,得到
,得到
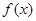 在
在 均为单调减函数.
均为单调减函数.
分 和
和 讨论得证.
讨论得证.
试题解析:(1)当 时,
时,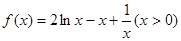
∵
∴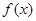 的减区间为
的减区间为 ,无增区间;
,无增区间;
(2)证明: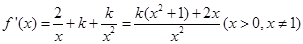 ,
,
因为, ,所以,
,所以,
故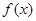 在
在 均为单调减函数.
均为单调减函数.
当 时,
时, ,而
,而 则
则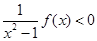 ;
;
当 时,
时, ,而
,而 则
则 ;
;
综上知,当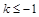 时,对所有的
时,对所有的 都有
都有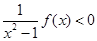 成立.
成立.
考点:应用导数研究函数的单调性

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
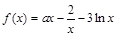 ,其中
,其中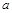 为常数.
为常数.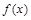 的图象在点
的图象在点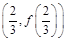 处的切线的斜率为1时,求函数
处的切线的斜率为1时,求函数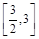 上的最小值;
上的最小值; 上既有极大值又有极小值,求实数
上既有极大值又有极小值,求实数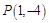 作函数
作函数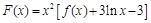 图象的切线,试问这样的切线有几条?并求这些切线的方程.
图象的切线,试问这样的切线有几条?并求这些切线的方程.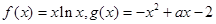 .
. 在
在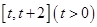 上的最小值;
上的最小值;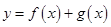 有两个不同的极值点
有两个不同的极值点 、
、 且
且 ,求实数
,求实数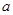 的取值范围.
的取值范围.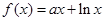 ,其中
,其中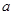 为常数,
为常数,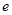 为自然对数的底数.
为自然对数的底数.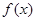 的单调区间;
的单调区间;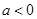 ,且
,且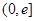 上的最大值为
上的最大值为 ,求
,求 时,试证明:
时,试证明: .
. .
. 的单调区间;
的单调区间; ,
, ,当
,当 时,有
时,有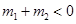 成立;
成立;
 恒成立.求实数
恒成立.求实数 的取值范围.
的取值范围. R,函数
R,函数 e
e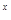 .
.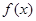 没有零点,求实数
没有零点,求实数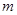 的取值范围;
的取值范围;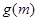 ,求
,求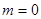 时,求证:
时,求证: .
.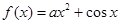 .
. 时,函数
时,函数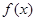 在
在 上单调递增;
上单调递增; .
.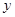 万元与投入
万元与投入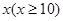 万元之间满足:
万元之间满足: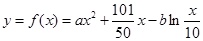 ,
,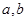 为常数,当
为常数,当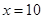 万元时,
万元时,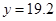 万元;当
万元;当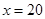 万元时,
万元时,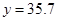 万元.(参考数据:
万元.(参考数据: ,
,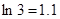 ,
, )
)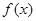 的解析式;
的解析式; 的最大值.(利润=旅游收入-投入)
的最大值.(利润=旅游收入-投入)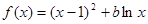 ,其中
,其中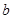 为常数。
为常数。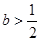 时,判断函数
时,判断函数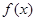 在定义域上的单调性;
在定义域上的单调性;