题目内容
设关于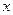 的函数
的函数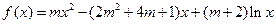 ,其中
,其中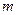 为
为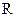 上的常数,若函数
上的常数,若函数 在
在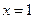 处取得极大值
处取得极大值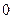
(1)求实数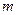 的值
的值
(2)若函数 的图像与直线
的图像与直线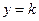 有两个交点,求实数
有两个交点,求实数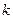 的取值范围
的取值范围
(3)设函数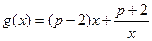 ,若对任意的
,若对任意的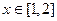 ,
,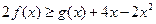 恒成立,求实数
恒成立,求实数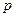 的取值范围.
的取值范围.
解:(1)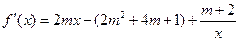
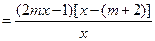
因为函数 在
在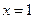 处取得极大值
处取得极大值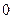
所以,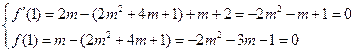 解
解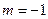
(2)由(Ⅰ)知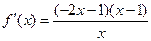 ,令
,令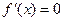 得
得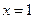 或
或 (舍去)
(舍去)
在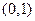 上函数
上函数 单调递增,在
单调递增,在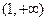 上函数
上函数 单调递减
单调递减
当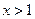 时,
时,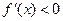 ,所以,函数
,所以,函数 在区间
在区间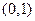 上单调递增,在区间
上单调递增,在区间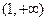 上单调递减,所以,当
上单调递减,所以,当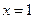 时,函数
时,函数 取得最大值,
取得最大值,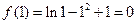
当 时,
时, 即
即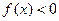
所以,当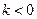 时,函数
时,函数 的图象与直线
的图象与直线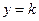 有两个交点,
有两个交点,
(3)设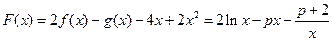
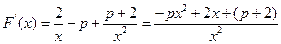
当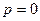 时,
时,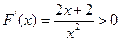 ,
,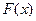 在
在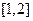 递增,
递增, 不成立,(舍)
不成立,(舍)
当 时
时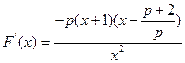
当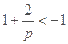 ,即
,即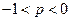 时,
时,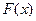 在
在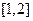 递增,
递增,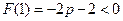 ,不成立
,不成立
当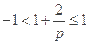 ,即
,即 时,
时,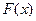 在
在 递增,所以
递增,所以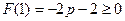 ,解得
,解得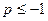 ,所以,此时
,所以,此时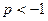
当 时,
时,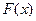 在
在 递增,成立;
递增,成立;
当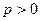 时,
时,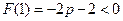 不成立 ,
不成立 ,
综上,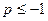
解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
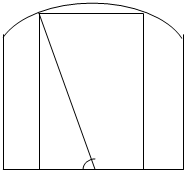 如图,钢板材料ABCD,上沿为圆弧AD,其所在圆的圆心为BC中点O,AB、CD都垂直于BC,且AB=CD=
如图,钢板材料ABCD,上沿为圆弧AD,其所在圆的圆心为BC中点O,AB、CD都垂直于BC,且AB=CD= 的函数
的函数 ,其中
,其中 为
为 上的常数,若函数
上的常数,若函数 在
在 处取得极大值
处取得极大值 .
. 有两个交点,求实数
有两个交点,求实数 的取值范围;
的取值范围; ,若对任意地
,若对任意地 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.