题目内容
下列命题中,真命题的是
①函数y=cos(2x+
)+1的图象的一个对称中心是(-
,0);
②要得到函数y=cos(-
+2x)的图象,只需将函数y=sin2x的图象向左平移
个单位;
③α=
+2kπ是tanα=1的充要条件;
④函数y=sinx-
cosx x∈[-π,0]的单调递增区间是[-
π, -
].
②
②
.①函数y=cos(2x+
| π |
| 2 |
| π |
| 2 |
②要得到函数y=cos(-
| π |
| 3 |
| π |
| 12 |
③α=
| π |
| 4 |
④函数y=sinx-
| 3 |
| 5 |
| 6 |
| π |
| 6 |
分析:函数y=cos(2x+
)+1的图象的对称中心满足:
;将函数y=sin2x的图象向左平移
个单位,得到y=sin(2x+
)=cos(
-2x)=cos(-
+2x)的图象;α=
+2kπ⇒tanα=1,tanα=1⇒α=
+kπ,或α=
+kπ,k∈Z,故α=
+2kπ是tanα=1的充分不必要条件;y=sinx-
cosx=2sin(x-
),x∈[-π,0]的增区间是[-
,0].
| π |
| 2 |
|
| π |
| 12 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| 3 |
| π |
| 3 |
| π |
| 6 |
解答:解:函数y=cos(2x+
)+1的图象的对称中心满足:
,故A不成立;
将函数y=sin2x的图象向左平移
个单位,
得到y=sin(2x+
)=cos(
-2x)=cos(-
+2x)的图象,故②成立;
α=
+2kπ⇒tanα=1,tanα=1⇒α=
+kπ,或α=
+kπ,k∈Z,
∴α=
+2kπ是tanα=1的充分不必要条件,故③不成立;
y=sinx-
cosx=2sin(x-
),x∈[-π,0]的增区间是[-
,0],故D不正确.
故答案为:②.
| π |
| 2 |
|
将函数y=sin2x的图象向左平移
| π |
| 12 |
得到y=sin(2x+
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
α=
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴α=
| π |
| 4 |
y=sinx-
| 3 |
| π |
| 3 |
| π |
| 6 |
故答案为:②.
点评:本题考查命题的真假判断及其应用,解题时要认真审题,注意三角函数的性质的灵活运用.

练习册系列答案
相关题目
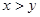 ,则
,则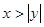 ”的逆命题
”的逆命题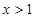 ,则
,则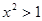 ”的否命题
”的否命题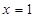 ,则
,则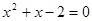 ”的否命题
”的否命题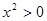 ,则
,则