题目内容
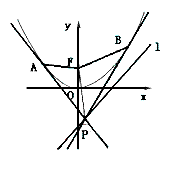
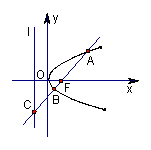
(理)如图,与抛物线x2=-4y相切于点A(-4,-4)的直线l分别交x轴、y轴于点F、E,过点E作y轴的垂线l0.
(1)若以l0为一条准线,中心在坐标原点的椭圆恰与直线l也相切,切点为T,求椭圆的方程及点T的坐标;
(2)若直线l与双曲线6x2-λy2=8的两个交点为M、N,且点A为线段MN的中点,又过点E的直线与该双曲线的两支分别交于P、Q两点,记![]() 在x轴正方向上的投影为p,且(
在x轴正方向上的投影为p,且(![]() )p2=m,m∈[
)p2=m,m∈[![]() ,
,![]() ],求(1)中切点T到直线PQ的距离的最小值.
],求(1)中切点T到直线PQ的距离的最小值.
(文)如图,与抛物线x2=-4y相切于点A(-4,-4)的直线l分别交x轴、y轴于点F、E,过点E作y轴的垂线l0.

(1)若以l0为一条准线,中心在坐标原点的椭圆恰好过点F,求椭圆的方程;
(2)若直线l与双曲线6x2-λy2=8的两个交点为M、N,且点A为线段MN的中点,又过点E的直线与该双曲线的两支分别交于P、Q两点,记![]() 在x轴正方向上的投影为p,且(
在x轴正方向上的投影为p,且(![]() )p2=m,m∈[
)p2=m,m∈[![]() ,
,![]() ],求直线PQ的斜率的取值范围.
],求直线PQ的斜率的取值范围.
答案:(理)解:抛物线x2=-4y中,∵导数y′=-![]() x,∴直线l的斜率为y′|x=-4=2.
x,∴直线l的斜率为y′|x=-4=2.
故直线l的方程为y=2x+4.∴点F、E的坐标分别为F(-2,0)、E(0,4).
(1)∵直线l0的方程是y=4,∴以l0为一条准线,中心在坐标原点的椭圆方程可设为![]() =1(a>b>0).则
=1(a>b>0).则![]() =4.由
=4.由
![]() (4b2+a2)x2+16b2x+16b2-a2b2=0.
(4b2+a2)x2+16b2x+16b2-a2b2=0.
∵直线l与椭圆相切,∴Δ=162b4-4(4b2+a2)(16b2-a2b2)=0.而![]() =4,a2=b2+c2,解得a2=4,b2=3.
=4,a2=b2+c2,解得a2=4,b2=3.
∴所求椭圆方程为![]() =1.
=1.
此时,x=![]() ,即切点T的坐标为T(-
,即切点T的坐标为T(-![]() ,1).
,1).
(2)设l与双曲线6x2-λy2=8的两个交点为M(x1,y1)、N(x2,y2),显然x1≠x2.∵点A为线段MN的中点,∴x1+x2=-8,y1+y2=-8.
由 .
.
而kl=![]() =
=![]() =2
=2![]() λ=3.∴双曲线的方程为6x2-3y2=8,即
λ=3.∴双曲线的方程为6x2-3y2=8,即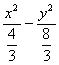 =1.
=1.
∵![]() 在x轴正方向上的投影为p,
在x轴正方向上的投影为p,
∴p2=cos2∠EFO=![]() .
.
设直线PQ的方程为y=kx+4(斜率k必存在),点P(x3,y3),Q(x4,y4).
∴![]() =x3x4+y3y4=
=x3x4+y3y4=![]() =5m.而m∈[
=5m.而m∈[![]() ,
,![]() ],∴
],∴![]() ≤
≤![]() =x3x4+y3y4≤
=x3x4+y3y4≤![]() .
.
由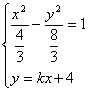
![]() (6-3k2)x2-24kx-56=0.∵P、Q两点分别在双曲线的两支上,∴6-3k2≠0.
(6-3k2)x2-24kx-56=0.∵P、Q两点分别在双曲线的两支上,∴6-3k2≠0.
∴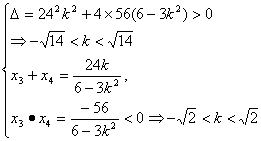 ∴
∴![]() .
.
此时y3y4=(kx3+4)(kx4+4)=k2x3x4+4k(x3+x4)+16.∴x3x4+y3y4=(1+k2)x3x4+4k(x3+x4)+16
=![]() (1+k2)+
(1+k2)+![]() =
=![]() =
=![]() .
.
∴![]() .∴
.∴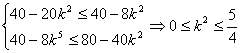 .
.![]() ,
,
∴k2∈[0,![]() ],即k∈[
],即k∈[![]() ,
,![]() ].
].
而切点T到直线PQ的距离为
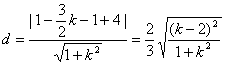
![]() .
.
设t=![]() ,k∈[
,k∈[![]() ],则t′=
],则t′=![]() .
.
令t′>0![]() k<-
k<-![]() 或k>2.∴t=
或k>2.∴t=![]() 在[
在[![]() ]上单调递增,在[-
]上单调递增,在[-![]() ,
,![]() ]上单调递减.
]上单调递减.
又k=![]() 时,d=2+
时,d=2+![]() ;k=
;k=![]() 时,d=2-
时,d=2-![]() .∴dmin=2
.∴dmin=2![]() ,即切点T到直线PQ的距离的最小值为2
,即切点T到直线PQ的距离的最小值为2![]() .
.
(文)解:抛物线x2=-4y中,∵导数y′=-![]() x,∴直线l的斜率为y′|x=-4=2.故直线l的方程为y=2x+4.
x,∴直线l的斜率为y′|x=-4=2.故直线l的方程为y=2x+4.
∴点F、E的坐标分别为F(-2,0)、E(0,4),
(此处也可用Δ=0求切线斜率,再写出方程)
(1)∵直线l0的方程是y=4,∴以l0为一条准线,经过点F,中心在坐标原点的椭圆方程可设为![]() =1(a>2).则c=
=1(a>2).则c=![]() ,其准线方程为y=
,其准线方程为y=![]() =
=![]() .由
.由![]() =4,得
=4,得![]() =4,化简得a4=16(a2-4),解得a2=8.∴椭圆方程为
=4,化简得a4=16(a2-4),解得a2=8.∴椭圆方程为![]() =1.
=1.
(2)设l与双曲线6x2-λy2=8的两个交点为M(x1,y1)、N(x2,y2),显然x1≠x2.∵点A为线段MN的中点,∴x1+x2=-8,y1+y2=-8.由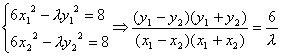 .
.
∵kl=![]() =
=![]() =2
=2![]() λ=3.∴双曲线的方程为6x2-3y2=8,即
λ=3.∴双曲线的方程为6x2-3y2=8,即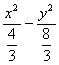 =1.
=1.
∵![]() 在x轴正方向上的投影为p,∴p2=cos2∠EFO=
在x轴正方向上的投影为p,∴p2=cos2∠EFO=![]()
=![]() .设直线PQ的方程为y=kx+4(斜率k必存在),点P(x3,y3),Q(x4,y4).
.设直线PQ的方程为y=kx+4(斜率k必存在),点P(x3,y3),Q(x4,y4).
∴![]() =x3x4+y3y4=
=x3x4+y3y4=![]() =5m.而m∈[
=5m.而m∈[![]() ,
,![]() ],∴
],∴![]() ≤
≤![]() =x3x4+y3y4≤
=x3x4+y3y4≤![]() .
.
由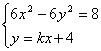
![]() (6-3k2)x2-24kx-56=0.∵P、Q两点分别在双曲线的两支上,∴6-3k2≠0.
(6-3k2)x2-24kx-56=0.∵P、Q两点分别在双曲线的两支上,∴6-3k2≠0.
∴ ∴
∴![]() .
.
此时y3y4=(kx3+4)(kx4+4)=k2x3x4+4k(x3+x4)+16.∴x3x4+y3y4=(1+k2)x3x4+4k(x3+x4)+16
=![]() (1+k2)+
(1+k2)+![]() +16=
+16=![]() =
=![]() .
.
∴![]() ≤
≤![]() ≤
≤![]() .∴
.∴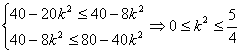 .
.
又![]() ,∴k2∈[0,
,∴k2∈[0,![]() ].∴k∈[
].∴k∈[![]() ].故所求直线PQ的斜率的取值范围是[
].故所求直线PQ的斜率的取值范围是[![]() ].
].