Question

（08年黄冈中学三模理）如图，设抛物线的准线与轴交于，焦点为；以为焦点，离心率的椭圆与抛物线在轴上方的一个交点为.

（Ⅰ）当时，求椭圆的方程及其右准线的方程；

（Ⅱ）在（Ⅰ）的条件下，直线经过椭圆的右焦点，与抛物线交于，如果

以线段为直径作圆，试判断点P与圆的位置关系，并说明理由；

（Ⅲ）是否存在实数，使得△的边长是连续的自然数，若存在，求出这样的实数；若不存在，请说明理由．

Answer 1

解析：（Ⅰ）设椭圆长半轴为，半焦距为，当时，，.

∵，∴

故椭圆方程为，右准线方程为    

（Ⅱ）依题意设直线的方程为：，R

联立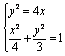  得点P的坐标为.

将代入得.

         设，由韦达定理得.

又,

      

   因为R,于是的值可能小于零,等于零,大于零,

即点可在圆内, 圆上或圆外.

（Ⅲ）假设存在满足条件的实数，

由题设有.

又设，有

设，对于抛物线，；

对于椭圆，，

即.

由 解得 ,

∴,    从而 .

因此，三角形的边长分别是 .

     所以时，能使三角形的边长是连续的自然数.