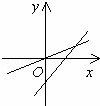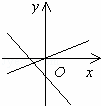题目内容
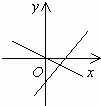
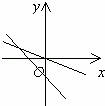
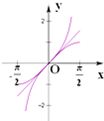
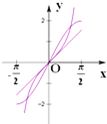
在同一直角坐标系中,表示直线y=ax与y=x+a正确的是( )
|
| A. |
| B. |
| C. |
| D. |
|
考点:
确定直线位置的几何要素.
专题:
数形结合.
分析:
本题是一个选择题,按照选择题的解法来做题,由y=x+a得斜率为1排除B、D,由y=ax与y=x+a中a同号知若y=ax递增,则y=x+a与y轴的交点在y轴的正半轴上;若y=ax递减,则y=x+a与y轴的交点在y轴的负半轴上,得到结果.
解答:
解:由y=x+a得斜率为1排除B、D,
由y=ax与y=x+a中a同号知若y=ax递增,则y=x+a与y轴的交点在y轴的正半轴上;
若y=ax递减,则y=x+a与y轴的交点在y轴的负半轴上;
故选C.
点评:
本题考查确定直线为主的几何要素,考查斜率和截距对于一条直线的影响,是一个基础题,这种题目也可以出现在直线与圆锥曲线之间的图形的确定.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目