题目内容
在平面直角坐标系中,已知向量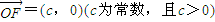 ,
,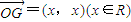 ,|
,|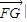 的最小值为1,
的最小值为1,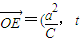 )(a为常数,且a>c,t∈R).动点P同时满足下列三个条件:
)(a为常数,且a>c,t∈R).动点P同时满足下列三个条件:(1)
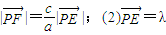 •
•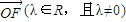 ;
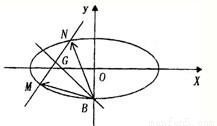
;(2)动点P的轨迹C经过点B(0,-1).
(Ⅰ)求曲线C的方程;
(Ⅱ)是否存在方向向量为m=(1,k)(k≠0)的直线l,l与曲线C相交于M、N两点,使|
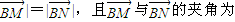 60°?若存在,求出k值,并写出直线l的方程;若不存在,请说明理由.
60°?若存在,求出k值,并写出直线l的方程;若不存在,请说明理由.
【答案】分析:(I)将|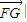 的长度用G的坐标表示成关于x的二次函数,通过求二次函数的最小值求出c的值.利用已知条件及唾液的第二定义判断出曲线C为椭圆,写出椭圆的方程.
的长度用G的坐标表示成关于x的二次函数,通过求二次函数的最小值求出c的值.利用已知条件及唾液的第二定义判断出曲线C为椭圆,写出椭圆的方程.
(II)将直线方程与椭圆方程联立,消去y得到关于x的二次方程,利用韦达定理,将转化为B在MN的中垂线上得到
m=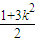 ,根据已知得到△BMN为等边三角形,得到点B到直线MN的距离d与|MN|的关系,利用点到直线的距离公式及弦长公式求出d与|MN|,列出方程求出k的值.
,根据已知得到△BMN为等边三角形,得到点B到直线MN的距离d与|MN|的关系,利用点到直线的距离公式及弦长公式求出d与|MN|,列出方程求出k的值.
解答:解(1)∵|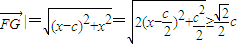 ,
,
∴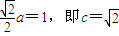
由 .
.
由(1)、(2)可知点P到直线x= ,再由椭圆的第二定义可知,点P的轨迹是椭圆,
,再由椭圆的第二定义可知,点P的轨迹是椭圆,
椭圆C的方程为: .
.
由(3)可知b=1,
∴a2=b2+c2=1+2=3.
∴椭圆C的方程为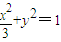 .
.
(2)设直线l的方程为:y=kx+m,设M(x1,y1),N(x2,y2) .
.
x1+x2=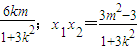
△=36k2m2-12(m2-1)(1+3k2)=12[3k2-m2+1]>0 ①
线段MN的中点G(x,y),
x=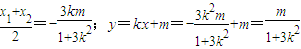 ,
,
线段MN的垂直平分线的方程为:y-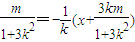
∵|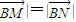 ,
,
∴线段MN的垂直平分线过B(0,-1)点,
∴-1-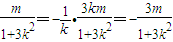 ,
,
∴m=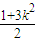 ②
②
②代入①,得3k2-( .③
.③
∵|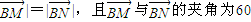 °,
°,
∴△BMN为等边三角形,
∴点B到直线MN的距离d=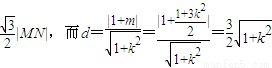
|MN|=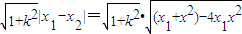
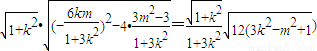
=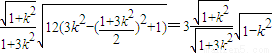
∴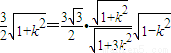 ,
,
解得k2=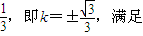 ③式.代入②,得m=
③式.代入②,得m=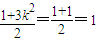 .
.
直线l的方程为:y=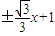
点评:解决直线与圆锥曲线的相交的有关问题,一般的思路是将直线与圆锥曲线方程联立,得到关于应该未知数的方程,利用韦达定理来解决.
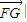 的长度用G的坐标表示成关于x的二次函数,通过求二次函数的最小值求出c的值.利用已知条件及唾液的第二定义判断出曲线C为椭圆,写出椭圆的方程.
的长度用G的坐标表示成关于x的二次函数,通过求二次函数的最小值求出c的值.利用已知条件及唾液的第二定义判断出曲线C为椭圆,写出椭圆的方程.(II)将直线方程与椭圆方程联立,消去y得到关于x的二次方程,利用韦达定理,将转化为B在MN的中垂线上得到
m=
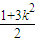 ,根据已知得到△BMN为等边三角形,得到点B到直线MN的距离d与|MN|的关系,利用点到直线的距离公式及弦长公式求出d与|MN|,列出方程求出k的值.
,根据已知得到△BMN为等边三角形,得到点B到直线MN的距离d与|MN|的关系,利用点到直线的距离公式及弦长公式求出d与|MN|,列出方程求出k的值.解答:解(1)∵|
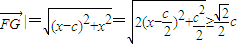 ,
,∴
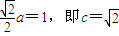

由
 .
.由(1)、(2)可知点P到直线x=
 ,再由椭圆的第二定义可知,点P的轨迹是椭圆,
,再由椭圆的第二定义可知,点P的轨迹是椭圆,椭圆C的方程为:
 .
.由(3)可知b=1,
∴a2=b2+c2=1+2=3.
∴椭圆C的方程为
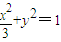 .
.(2)设直线l的方程为:y=kx+m,设M(x1,y1),N(x2,y2)
 .
.x1+x2=
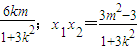
△=36k2m2-12(m2-1)(1+3k2)=12[3k2-m2+1]>0 ①
线段MN的中点G(x,y),
x=
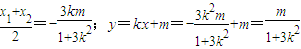 ,
,线段MN的垂直平分线的方程为:y-
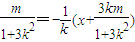
∵|
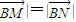 ,
,∴线段MN的垂直平分线过B(0,-1)点,
∴-1-
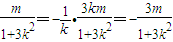 ,
,∴m=
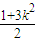 ②
②②代入①,得3k2-(
 .③
.③∵|
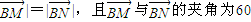 °,
°,∴△BMN为等边三角形,
∴点B到直线MN的距离d=
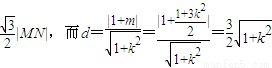
|MN|=
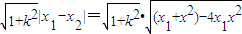
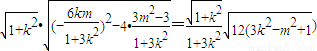
=
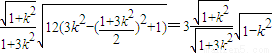
∴
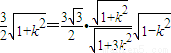 ,
,解得k2=
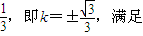 ③式.代入②,得m=
③式.代入②,得m=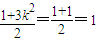 .
.直线l的方程为:y=
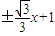
点评:解决直线与圆锥曲线的相交的有关问题,一般的思路是将直线与圆锥曲线方程联立,得到关于应该未知数的方程,利用韦达定理来解决.

练习册系列答案
相关题目