题目内容
已知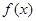 是周期为2的奇函数,当
是周期为2的奇函数,当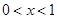 时,
时,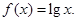
设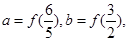
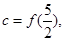 则( )
则( )
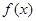 是周期为2的奇函数,当
是周期为2的奇函数,当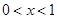 时,
时,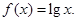
设
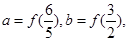
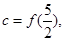 则( )
则( )A.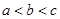 | B.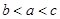 | C.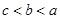 | D.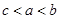 |
D
考点:
分析:首先利用奇函数的性质与函数的周期性把f(x)的自变量转化到区间(0,1)内,然后由对数函数f(x)=lgx的单调性解决问题.
解答:解:已知f(x)是周期为2的奇函数,当0<x<1时,f(x)=lgx.
则a=f( )=f(-
)=f(- )=-f(
)=-f( )=-lg
)=-lg >0,
>0,
b=f( )=f(-
)=f(- )=-f(
)=-f( )=-lg
)=-lg >0,
>0,
c=f( )=f(
)=f( )=lg
)=lg <0,
<0,
又lg >lg
>lg
∴0<-lg <-lg
<-lg
∴c<a<b,
故选D.
点评:本题主要考查奇函数性质与函数的周期性,同时考查对数函数的单调性.
分析:首先利用奇函数的性质与函数的周期性把f(x)的自变量转化到区间(0,1)内,然后由对数函数f(x)=lgx的单调性解决问题.
解答:解:已知f(x)是周期为2的奇函数,当0<x<1时,f(x)=lgx.
则a=f(
 )=f(-
)=f(- )=-f(
)=-f( )=-lg
)=-lg >0,
>0,b=f(
 )=f(-
)=f(- )=-f(
)=-f( )=-lg
)=-lg >0,
>0,c=f(
 )=f(
)=f( )=lg
)=lg <0,
<0,又lg
 >lg
>lg
∴0<-lg
 <-lg
<-lg
∴c<a<b,
故选D.
点评:本题主要考查奇函数性质与函数的周期性,同时考查对数函数的单调性.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
 。
。 的导数
的导数 ;
; 满足
满足 。
。 的解析式;
的解析式; 上,
上,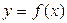
 的图象恒在
的图象恒在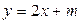 的图象上方,试确定实数
的图象上方,试确定实数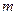 的取值范围。
的取值范围。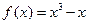 ,其图像记为
,其图像记为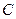 ,若对于任意非零实数
,若对于任意非零实数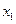 ,曲线
,曲线 处的切线交于另一点
处的切线交于另一点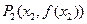 ,曲线
,曲线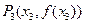 ,线段
,线段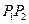 ,
,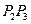 与曲线
与曲线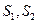 ,求证:
,求证: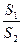 为定值;
为定值;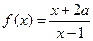 在区间
在区间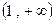 上单调递增,则实数
上单调递增,则实数
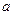 的取值范围为
的取值范围为  点,则每根铁筋的长度为________米.
点,则每根铁筋的长度为________米. 
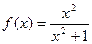 的值域为 .
的值域为 .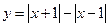 的最大值是
的最大值是 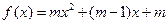 有零点,则实数
有零点,则实数 的取值范围是
的取值范围是  __
__