Question

13．在曲线y=x²（x≥0）上某一点A处做一切线使之与曲线以及x轴所围成的面积为$\frac{1}{12}$，则切点A的坐标为（1，1）．

Answer 1

分析 先求切点A的坐标，设点A的坐标为（a，a²），故先利用导数求出在切点处的导函数值，再结合导数的几何意义即可求出切线的斜率，从而得到切线的方程进而求得面积的表达式．建立关于a的方程解之即得切点A的坐标．

解答 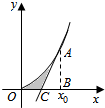解：设点A的坐标为（a，a²），
过点A的切线的斜率为k=y'|_x=a=2a，
故过点A的切线l的方程为y-a²=2a（x-a），
即y=2ax-a²，令y=0，得x=$\frac{a}{2}$，
则S=S_△ABO-S_△ABC=-（$\frac{1}{2}$•$\frac{a}{2}$•a²-${∫}_{0}^{a}$x²dx）=$\frac{{a}^{3}}{12}$=$\frac{1}{12}$，
∴a=1，
∴切点A的坐标为（1，1），
故答案为：（1，1）．

点评 本题主要考查利用导数研究曲线上某点切线方程、定积分的应用、直线的方程等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于中档题．