题目内容
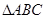 中,
中,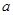 、
、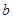 、
、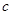 分别是角
分别是角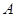 、
、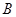 、
、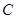 的对边,若
的对边,若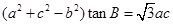 ,则角
,则角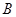 的值为__________.
的值为__________. 或
或
试题分析:因为
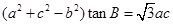 ,所以
,所以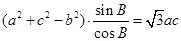 ,根据余弦定理有:
,根据余弦定理有: ,所以
,所以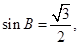 因为
因为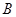 是三角形的内角,所以
是三角形的内角,所以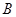 的值为
的值为 或
或 .
.点评:利用正余弦定理解三角形几乎是每年高考的必考内容,一定要熟练应用。另外,求出三角函数值之后,一定要先交代角的范围然后才能求角.

练习册系列答案
相关题目
题目内容
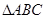 中,
中,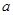 、
、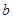 、
、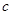 分别是角
分别是角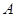 、
、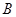 、
、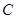 的对边,若
的对边,若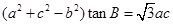 ,则角
,则角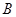 的值为__________.
的值为__________. 或
或
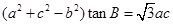 ,所以
,所以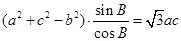 ,根据余弦定理有:
,根据余弦定理有: ,所以
,所以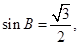 因为
因为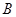 是三角形的内角,所以
是三角形的内角,所以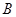 的值为
的值为 或
或 .
.