题目内容
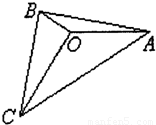
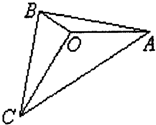如图，O是△ABC内的一点，∠AOB=150°，∠AOC=120°，向量| OA |
| OB |
| OC |
（1）求|
| OA |
| OB |
| OC |
（2）若
| OC |
| OA |
| OB |
分析：（1）求向量的模，先平方再开方，利用向量的数量积运算，可得结论；
（2）
=m
，
=n
，由向量加法及数乘向量的几何意义m＜0，n＜0，且∠COB′=90°，∠CB′D=30°，从而可建立方程，即可求实数m，n的值．
（2）
| OA′ |
| OA |
| OB′ |
| OB |
解答：解：（1）∵∠AOB=150°，∠AOC=120°，向量
，
，
的模分别为2、1、3．
∴
•
=-
，
•
=-3，
•
=0
∴|
+
+
|2=
2+
2+
2+2（
•
+
•
+
•
）=8-2
∴|
+
+
|=
；
（2）
=m
，
=n
，由向量加法及数乘向量的几何意义m＜0，n＜0，且∠COB′=90°，∠CB′D=30°
∴|
|2=|
|2+|
|2，且2|
|=|
|
∴4m2=n2+9，且6=2|m|
∴m=-3，n=-3
．
| OA |
| OB |
| OC |
∴
| OA |
| OB |
| 3 |
| OA |
| OC |
| OC |
| OB |
∴|
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
| OA |
| OB |
| OA |
| OC |
| OC |
| OB |
| 3 |
∴|
| OA |
| OB |
| OC |
8-2
|
（2）
| OA′ |
| OA |
| OB′ |
| OB |
∴|
| B′C |
| OC′ |
| OB′ |
| OC |
| OA′ |
∴4m2=n2+9，且6=2|m|
∴m=-3，n=-3
| 3 |
点评：本题考查向量知识的运用，考查向量的模，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
如图，已知△ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行四边形，DC⊥平面ABC，AB=2，如图，
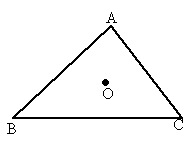
O是△ABC内一点，且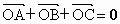
，则O是△ABC的
[
]
|
A ．内心 |
B ．外心 |
C ．重心 |
D ．垂心 |
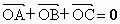，则O是△ABC的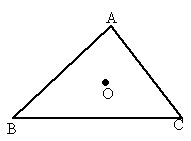
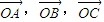的模分别为2、1、3．
；
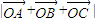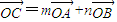，求实数m，n的值．