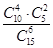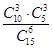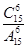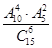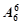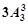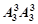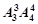题目内容
用1、2、3、4、5、6、7、8组成没有重复数字的八位数,要求1与2 相邻,3与4相邻,5与6相邻,而7与8不相邻,这样的八位数共有 个.(用数字作答)
576
试题分析:首先把1和2相邻,3与4相邻,5与6相邻当做三个元素进行排列有A33种结果,这三个元素形成四个空,把7和8 在这四个位置排列有A42种结果,三对相邻的元素内部各还有一个排列A22,根据分步计数原理得到这种数字的总数有A33A42A22A22A22=576,故答案为:576。
点评:相邻问题一般采用捆绑法,应用捆绑法解决排列组合问题时,一定要注意“捆绑”起来的元素内部的顺序。不相邻问题一般采用插空法。

练习册系列答案
相关题目
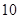 个图案中需用黑色瓷砖 块.
个图案中需用黑色瓷砖 块.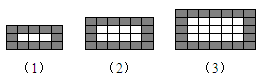

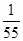
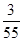
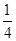
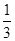
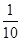 B.
B.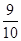 C.
C.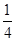 D.
D.