题目内容
函数y=cos2x在下列哪个区间上是减函数( )A.[-
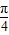 ,
,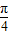 ]
]B.[
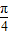 ,
,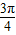 ]
]C.[0,
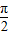 ]
]D.[
 ,π]
,π]
【答案】分析:将2x看做一个整体,令kπ≤x≤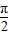 +kπ(k∈Z)解出x的范围后,对选项逐一验证即可.
+kπ(k∈Z)解出x的范围后,对选项逐一验证即可.
解答:解:∵y=cos2x∴2kπ≤2x≤π+2kπ(k∈Z)
∴kπ≤x≤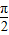 +kπ(k∈Z)
+kπ(k∈Z)
当k=0时,0≤x≤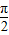 函数y=cos2x单调递减
函数y=cos2x单调递减
故选C.
点评:本题主要考查余弦函数的单调问题,一般把wx+ρ看做一个整体,确定满足的不等式后解x的范围.
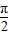 +kπ(k∈Z)解出x的范围后,对选项逐一验证即可.
+kπ(k∈Z)解出x的范围后,对选项逐一验证即可.解答:解:∵y=cos2x∴2kπ≤2x≤π+2kπ(k∈Z)
∴kπ≤x≤
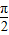 +kπ(k∈Z)
+kπ(k∈Z)当k=0时,0≤x≤
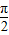 函数y=cos2x单调递减
函数y=cos2x单调递减故选C.
点评:本题主要考查余弦函数的单调问题,一般把wx+ρ看做一个整体,确定满足的不等式后解x的范围.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
函数y=cos2x在下列哪个区间上是减函数( )
A、[-
| ||||
B、[
| ||||
C、[0,
| ||||
D、[
|
函数y=cos2x在点(
,0)处的切线方程是( )
| π |
| 4 |
| A、4x+2y+π=0 |
| B、4x-2y+π=0 |
| C、4x-2y-π=0 |
| D、4x+2y-π=0 |