题目内容
(本小题满分12分)
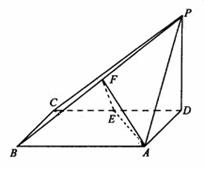
如图，四棱锥P—ABCD中，底面ABCD为矩形，PD⊥底面ABCD，AD=PD=1，AB=
BC，E、F分别为CD、PB的中点.
|
（2）求三棱锥
的体积。.
（1）证明：连结EP，
∵PD⊥底面ABCD，DE在平面ABCD内，∴PD⊥DE，又CE=ED，PD=AD=BC，
∴Rt△BCE≌Rt△PDE.∴PE=BE.
∵F为PB中点，∴EF⊥PB.
∵AB⊥平面PAD ∴PA⊥AB.
∴在Rt△PAB中PF=AF，又PE=BE=EA，
∴△EFP≌△EFA,∴EF⊥FA.
∵PB、FA为平面PAB内的相交直线. ∴EF⊥平面PAB. …………………6分
（2）∵EF⊥PB且PB⊥AF，∴PB⊥平面AEF………………………………………8分
直角三角形AEF中，∵EF=
,AF=1, ∴
，PF=1……………10分
∴
……………………………………12分
练习册系列答案
津桥教育计算小状元系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
