题目内容
(2012•芜湖三模)某校考生参加2012年全国高校自主招生考试,假设每位考生只能申请A,B,C三所大学中的一所,且申请其中任意一所大学都是等可能的,现有4位考生申请参加自主招生考试.
(Ⅰ)求恰有2人申请A大学的概率;
(Ⅱ)求4人申请大学数量ξ的概率分布和数学期望.
(Ⅰ)求恰有2人申请A大学的概率;
(Ⅱ)求4人申请大学数量ξ的概率分布和数学期望.
分析:(I)所有可能的方式有34种,恰有2人申请A大学的申请方式有
•22种,从而然后利用概率公式进行求解;
(II)ξ=1,2,3,然后分别求出相应的概率,列出分布列,根据数学期望公式进行求解即可;
| C | 2 4 |
(II)ξ=1,2,3,然后分别求出相应的概率,列出分布列,根据数学期望公式进行求解即可;
解答:解:(I)所有可能的方式有34种,恰有2人申请A大学的申请方式有
•22种,
从而恰有2人申请A大学的概率为
=
.
(II)ξ=1,2,3,P(ξ=1)=
=
;
P(ξ=2)=
=
;
P(ξ=3)=
=
,
申请大学数量ξ的概率分布:
Eξ=1×
+2×
+3×
=
.
| C | 2 4 |
从而恰有2人申请A大学的概率为
| ||
| 34 |
| 8 |
| 27 |
(II)ξ=1,2,3,P(ξ=1)=
| 3 |
| 34 |
| 1 |
| 27 |
P(ξ=2)=
| ||||||||||
| 34 |
| 14 |
| 27 |
P(ξ=3)=
| ||||||||
| 34 |
| 4 |
| 9 |
申请大学数量ξ的概率分布:
| ξ | 1 | 2 | 3 | ||||||
| P |
|
|
|
| 1 |
| 27 |
| 14 |
| 27 |
| 4 |
| 9 |
| 65 |
| 27 |
点评:考查运用概率、离散型随机变量的期望与方差知识及解决实际问题的能力,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
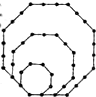 (2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是
(2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是