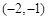题目内容
(本题16分)已知函数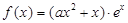 ,其中e是自然数的底数,
,其中e是自然数的底数,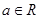 ,
,
(1)当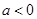 时,解不等式
时,解不等式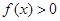 ;
;
(2)若当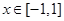 时,不等式
时,不等式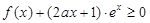 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(3)当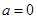 时,试判断:是否存在整数k,使得方程
时,试判断:是否存在整数k,使得方程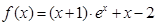 在
在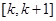
上有解?若存在,请写出所有可能的k的值;若不存在,说明理由。
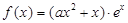 ,其中e是自然数的底数,
,其中e是自然数的底数,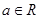 ,
,(1)当
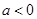 时,解不等式
时,解不等式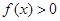 ;
;(2)若当
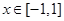 时,不等式
时,不等式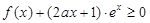 恒成立,求a的取值范围;
恒成立,求a的取值范围;(3)当
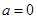 时,试判断:是否存在整数k,使得方程
时,试判断:是否存在整数k,使得方程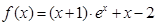 在
在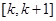
上有解?若存在,请写出所有可能的k的值;若不存在,说明理由。
(1)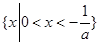 ;(2)
;(2)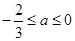 ;(3)存在唯一的整数
;(3)存在唯一的整数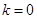 。
。
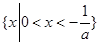 ;(2)
;(2)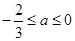 ;(3)存在唯一的整数
;(3)存在唯一的整数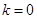 。
。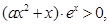 因为
因为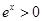 所以
所以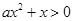 ,
,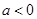 取根的中间;
取根的中间;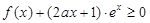 即不等式
即不等式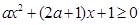 恒成立,分类讨论:
恒成立,分类讨论: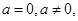 且
且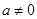 时,
时,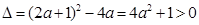
数形结合:
如图:
若
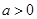 ,
,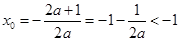
,
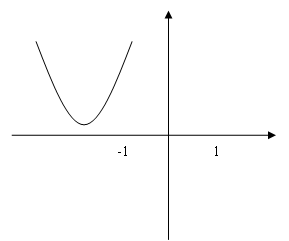
若
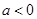 ,如图:
,如图: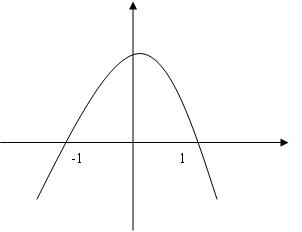
(4)方程
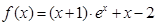 在
在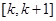
上有解,需判断函数在
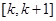 上的单调性,数形结合。
上的单调性,数形结合。(1)
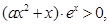 即
即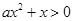 ,由于
,由于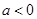 ,所以
,所以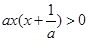
所以解集为
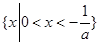 ;
;(2)当
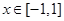 时,即不等式
时,即不等式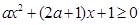 恒成立,
恒成立,①若
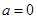 ,则
,则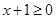 ,该不等式满足在
,该不等式满足在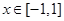 时恒成立;
时恒成立;②由于
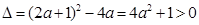 ,
,所以
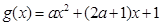 有两个零点,
有两个零点,若
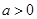 ,则需满足
,则需满足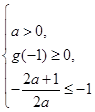 即
即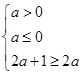 ,此时
,此时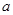 无解;
无解;③若
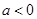 ,则需满足
,则需满足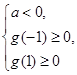 ,即
,即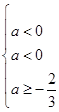 ,所以
,所以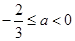 ,
,综上所述,a的取值范围是
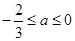 。
。(3)方程即为
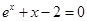 ,设
,设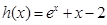 ,
,由于
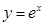 和
和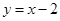 均为增函数,则
均为增函数,则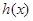 也是增函数,
也是增函数,又因为
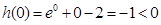 ,
,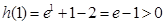 ,
,所以该函数的零点在区间
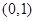 上,又由于函数为增函数,所以该函数有且仅有
上,又由于函数为增函数,所以该函数有且仅有一个零点,所以方程
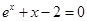 有且仅有一个根,且在
有且仅有一个根,且在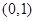 内,所以存在唯
内,所以存在唯一的整数
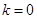 。
。
练习册系列答案
相关题目
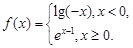 ,若
,若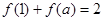 ,则
,则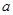 的所有可能值为 .
的所有可能值为 .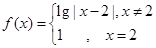 ,若关于
,若关于 的方程
的方程 恰有5个不同的实数解
恰有5个不同的实数解 ,则
,则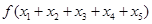 等于 ( )
等于 ( )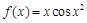 在区间
在区间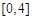 上的零点个数为
上的零点个数为 若函数
若函数 有三个零点,则实数
有三个零点,则实数 的值是 .
的值是 .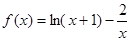 的零点所在
的零点所在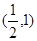
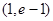
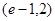
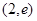
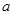 满足
满足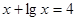 ,
,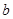 满足
满足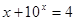 ,函数
,函数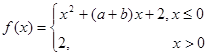 ,则关于
,则关于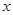 的方程
的方程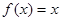 的解的个数是
的解的个数是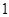
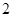
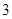
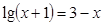 的解为
的解为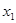 ,方程
,方程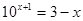 的解为
的解为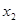 ,则
,则 ( )
( )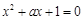 的一个实根在区间
的一个实根在区间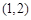 内,则
内,则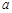 的取值范围为
的取值范围为