题目内容
已知函数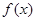 的图象在
的图象在 上连续,定义:
上连续,定义: ,
, .其中,
.其中,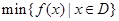 表示函数
表示函数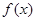 在
在 上的最小值,
上的最小值,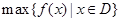 表示函数
表示函数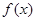 在
在 上的最大值.若存在最小正整数
上的最大值.若存在最小正整数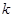 ,使得
,使得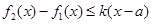 对任意的
对任意的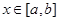 成立,则称函数
成立,则称函数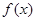 为
为 上的“
上的“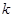 阶收缩函数”.
阶收缩函数”.
(Ⅰ)若 ,试写出
,试写出 ,
,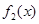 的表达式;
的表达式;
(Ⅱ)已知函数 ,试判断
,试判断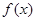 是否为
是否为 上的“
上的“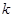 阶收缩函数”.如果是,求出对应的
阶收缩函数”.如果是,求出对应的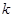 ;如果不是,请说明理由;
;如果不是,请说明理由;
(Ⅲ)已知 ,函数
,函数 是
是 上的2阶收缩函数,求
上的2阶收缩函数,求 的取值范围.
的取值范围.
(Ⅰ)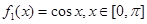 ,
, ;(Ⅱ)存在k=4,使得f(x)是[﹣1,4]上的4阶收缩函数.(Ⅲ)
;(Ⅱ)存在k=4,使得f(x)是[﹣1,4]上的4阶收缩函数.(Ⅲ)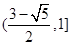
【解析】
试题分析:(Ⅰ)根据f(x)=cosx的最大值为1,可得f1(x)、f2(x)的解析式.
(Ⅱ)根据函数f(x)=x2在x∈[-1,4]上的值域,先写出f1(x)、f2(x)的解析式,再由f2(x)-f1(x)≤k(x-a)求出k的范围得到答案.
(3)先对函数f(x)进行求导判断函数的单调性,进而写出f1(x)、f2(x)的解析式,
然后再由f2(x)-f1(x)≤k(x-a)求出k的范围得到答案.
试题解析:
(Ⅰ)由题意可得: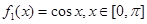 ,
, 2分
2分
(Ⅱ) ,
,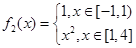 ,
,
所以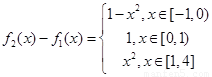 4分
4分
当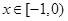 时,
时,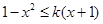 ,∴
,∴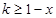 ,即
,即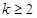 ;
;
当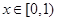 时,
时,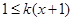 ,∴
,∴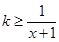 ,即
,即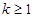 ;
;
当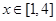 时,
时,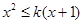 ,∴
,∴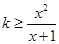 ,即
,即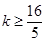 .
.
综上所述,∴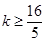
即存在k=4,使得f(x)是[﹣1,4]上的4阶收缩函数. 7分
(Ⅲ)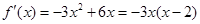 令
令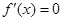 得
得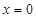 或
或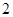 .函数f(x)的变化情况如下:
.函数f(x)的变化情况如下:
|
x |
(- |
0 |
(0,2) |
2 |
(2,+ |
|
|
- |
0 |
+ |
0 |
- |
|
f(x) |
|
0 |
|
4 |
|
令f(x)=0,解得x=0或3.
(ⅰ)b≤2时,f(x)在[0,b]上单调递增,因此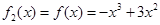 ,
,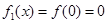 .
.
因为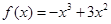 是[0,b]上的2阶收缩函数,所以,①
是[0,b]上的2阶收缩函数,所以,①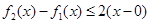 对x∈[0,b]恒成立;②存在x∈[0,b],使得
对x∈[0,b]恒成立;②存在x∈[0,b],使得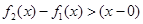 成立.
成立.
①即: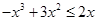 对x∈[0,b]恒成立,由
对x∈[0,b]恒成立,由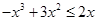 ,解得:0≤x≤1或x≥2,
,解得:0≤x≤1或x≥2,
要使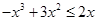 对x∈[0,b]恒成立,需且只需0<b≤1.
对x∈[0,b]恒成立,需且只需0<b≤1.
②即:存在x∈[0,b],使得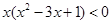 成立.由
成立.由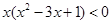 得:x<0或
得:x<0或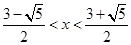 ,所以
,所以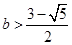 .
.
综合①②可得: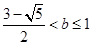 .
10分
.
10分
(ⅱ)当b>2时,显然有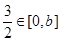 ,由于f(x)在[0,2]上单调递增,根据定义可得:
,由于f(x)在[0,2]上单调递增,根据定义可得: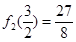 ,
,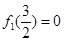 ,可得
,可得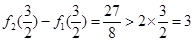 ,
,
此时,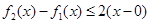 不成立.
12分
不成立.
12分
综合ⅰ)ⅱ)可得: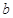 的取值范围为
的取值范围为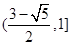 .
13分
.
13分
(注:在(ⅱ)中只要取区间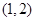 内的一个数来构造反例即可,这里用
内的一个数来构造反例即可,这里用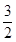 只是因为简单而已)
只是因为简单而已)
考点:1.函数的导数;2.导数的性质的应用.3.不等式.

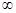 ,0)
,0)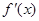
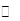
 已知
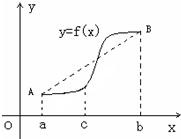
已知 (2)如右图所示,若函数
(2)如右图所示,若函数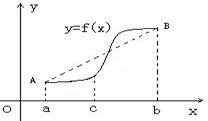 (Ⅰ)若f(x)在
(Ⅰ)若f(x)在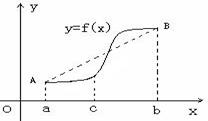 (Ⅰ)若f(x)在
(Ⅰ)若f(x)在