题目内容
 已知f(x)=
已知f(x)=| 2 |
| 3 |
(1)若f(x)在x=1+
| 2 |
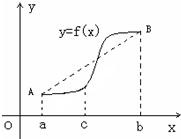
(2)如图所示,若函数y=f(x)的图象在[a,b]连续光滑,试猜想拉格朗日中值定理:即一定存在c∈(a,b),使得f′(c)=
| f(b)-f(a) |
| b-a |
分析:(1)先求f′(x)由f′(1+
)=0,求得c,再用f′(x)>0求得增区间.
(2)先化简g(x)=ex-e2-x+f(x)═ex-e2-x+
x3-2x2-2x+4,则g′(x)=ex+
+2(x-1)2-4≥2
+2•0-4=2e-4.由猜想知对于函数y=g(x)图象上任意两点A、B,在A、B之间一定存在一点C(c,g′(c)),有g′(x)≥2e-4.
| 2 |
(2)先化简g(x)=ex-e2-x+f(x)═ex-e2-x+
| 2 |
| 3 |
| e2 |
| ex |
ex•
|
解答:解:(1)f′(x)=2x2-4x+c,(1分)
依题意,有f′(1+
)=0,即c=-2(1+
)2+4(1+
)=-2.(2分)
∴f(x)=
x3-2x2-2x+4,f′(x)=2x2-4x-2.
令f′(x)>0,得x<1-
或x>1+
,(5分)
从而f(x)的单调增区间为:(-∞,1-
]及[1+
,+∞);(6分)
(2)f′(c)=
;g(x)=ex-e2-x+f(x)═ex-e2-x+
x3-2x2-2x+4,(7分)
g′(x)=ex+e2-x+2x2-4x-2(9分)=ex+
+2(x-1)2-4≥2
+2•0-4=2e-4.(12分)
由(2)知,对于函数y=g(x)图象上任意两点A、B,在A、B之间一定存在一点C(c,g′(c)),使得g′(c)=KAB,又g′(x)≥2e-4,故有KAB=g′(c)≥2e-4,证毕.(14分)
依题意,有f′(1+
| 2 |
| 2 |
| 2 |
∴f(x)=
| 2 |
| 3 |
令f′(x)>0,得x<1-
| 2 |
| 2 |
从而f(x)的单调增区间为:(-∞,1-
| 2 |
| 2 |
(2)f′(c)=
| f(b)-f(a) |
| b-a |
| 2 |
| 3 |
g′(x)=ex+e2-x+2x2-4x-2(9分)=ex+
| e2 |
| ex |
ex•
|
由(2)知,对于函数y=g(x)图象上任意两点A、B,在A、B之间一定存在一点C(c,g′(c)),使得g′(c)=KAB,又g′(x)≥2e-4,故有KAB=g′(c)≥2e-4,证毕.(14分)
点评:本题主要考查导数问题一是用导数研究函数的单调性二是考查导数的几何意义.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案
相关题目