题目内容
函数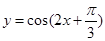 定义域为
定义域为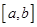 ,值域为
,值域为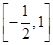 ,则
,则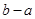 的最大值与最小值之和为( )
的最大值与最小值之和为( )
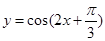 定义域为
定义域为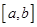 ,值域为
,值域为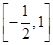 ,则
,则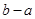 的最大值与最小值之和为( )
的最大值与最小值之和为( )A.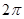 | B.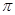 | C.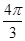 | D. |
B
试题分析:令
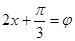 ,所以
,所以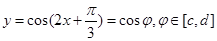 ,结合余弦函数的图象可知,要满足值域为
,结合余弦函数的图象可知,要满足值域为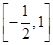 ,需要
,需要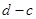 的最大值为
的最大值为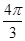 ,最小值为
,最小值为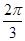 ,所以最大值与最小值之和为
,所以最大值与最小值之和为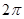 ,所以
,所以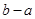 的最大值与最小值之和为
的最大值与最小值之和为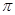 .
.点评:为了画图方便,可以先令
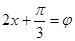 ,最后再还原回去.
,最后再还原回去.
练习册系列答案
相关题目
题目内容
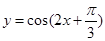 定义域为
定义域为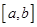 ,值域为
,值域为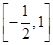 ,则
,则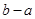 的最大值与最小值之和为( )
的最大值与最小值之和为( )A.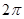 | B.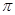 | C.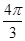 | D. |
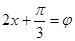 ,所以
,所以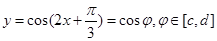 ,结合余弦函数的图象可知,要满足值域为
,结合余弦函数的图象可知,要满足值域为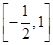 ,需要
,需要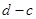 的最大值为
的最大值为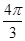 ,最小值为
,最小值为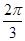 ,所以最大值与最小值之和为
,所以最大值与最小值之和为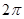 ,所以
,所以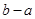 的最大值与最小值之和为
的最大值与最小值之和为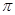 .
.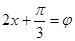 ,最后再还原回去.
,最后再还原回去.