题目内容
7.三角形与四面体有着类似的特征.如图1,△ABC中,若AD是∠BAC的角平分线,则$\frac{DB}{DC}=\frac{AB}{AC}$.依此类比:如图2,三棱锥S-PQR中,点M在QR上,若二面角Q-SP-M的大小等于二面角R-SP-M的大小,则$\frac{MQ}{MR}$=$\frac{{S}_{△PSQ}}{{S}_{△PSR}}$.
分析 将类比中的情景置于特殊情况之中,据此得出“类比结论”,这是解此类问题的常用方法.
解答 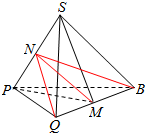 解:不妨设QP=QS,RP=RS,
解:不妨设QP=QS,RP=RS,
再取PS的中点N,则QN⊥PS,RN⊥PS,如右图:
因为,△SQR≌△PQR,所以,MP=MS,
所以,MN⊥PS,因此根据几何关系可知,
二面角Q-SP-M的平面角为:∠QNM,
二面角R-SP-M的平面角为:∠RNM,
因为以上两个二面角角的平面相等,即∠QNM=∠RNM,
即NM平分∠QNR,根据角平分线定理,
$\frac{MQ}{MR}$=$\frac{NQ}{NR}$=$\frac{{S}_{△PSQ}}{{S}_{△PSR}}$,
故可填(答案不唯一):$\frac{{S}_{△PSQ}}{{S}_{△PSR}}$.
点评 本题主要考查了合情推理中的类比推理,涉及二面角平面的定义和运算,猜测与验证,属于中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
17.若圆心在x轴上,半径为$\sqrt{5}$的圆C位于y轴左侧,且被直线x+2y=0截得的弦长为4,则圆C的方程是( )
| A. | ${(x-\sqrt{5})^2}+{y^2}=5$ | B. | ${(x+\sqrt{5})^2}+{y^2}=5$ | C. | (x-5)2+y2=5 | D. | (x+5)2+y2=5 |
18.设点A为抛物线y2=4x上一点B(1,0),且AB=1,则A的横坐标的值( )
| A. | -2 | B. | 0 | C. | -2或0 | D. | -2或2 |
19.已知f(sinx)=cos3x,x∈[-90°,90°],则f(cos10°)的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
17.cos(-$\frac{67}{6}$π)的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |