题目内容
已知函数f（x）=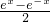
，则它是 ________函数（填“奇”或者“偶”），在R上单调递 ________
奇 增
分析：①求f（-x），看f（-x）与f（x）的关系来判断f（x）的奇偶性
②利用一个增函数减去一个减函数得到的新函数为增函数，可得f（x）是增函数．
解答：∵f（-x）=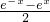
=-f（x）
∴f（x）是奇函数
∵y=ex是增函数，y=e-x是减函数．
∴f（x）是增函数．
故答案为：奇，增．
点评：本题考查了函数的单调性和奇偶性．判断函数的奇偶性时，应先确定定义域是否关于原点对称：关于原点对称，再看f（-x）与f（x）的关系，若f（-x）=f（x）是偶函数，若f（-x）=-f（x）是奇函数．定义域不关于原点对称，不存在奇偶性．
分析：①求f（-x），看f（-x）与f（x）的关系来判断f（x）的奇偶性
②利用一个增函数减去一个减函数得到的新函数为增函数，可得f（x）是增函数．
解答：∵f（-x）=
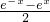=-f（x）∴f（x）是奇函数
∵y=ex是增函数，y=e-x是减函数．
∴f（x）是增函数．
故答案为：奇，增．
点评：本题考查了函数的单调性和奇偶性．判断函数的奇偶性时，应先确定定义域是否关于原点对称：关于原点对称，再看f（-x）与f（x）的关系，若f（-x）=f（x）是偶函数，若f（-x）=-f（x）是奇函数．定义域不关于原点对称，不存在奇偶性．
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|