题目内容
某班学生春假需要选择春游线路,已知甲寝室与乙寝室各有6位同学,每人选择一条线路.甲寝室选择去乌镇游玩的有1人,选择去横店游玩的有5人,乙寝室选择去乌镇游玩的有2人,选择去横店游玩的有4人,现从甲寝室、乙寝室中各任选2人分析游玩线路问题.
(Ⅰ)求选出的4人均选择游玩横店的概率;
(Ⅱ)设ξ 为选出的4个人中选择游玩乌镇的人数,求ξ 的分布列和数学期望Eξ
(Ⅰ)求选出的4人均选择游玩横店的概率;
(Ⅱ)设ξ 为选出的4个人中选择游玩乌镇的人数,求ξ 的分布列和数学期望Eξ
(Ⅰ)设“从甲寝室选出的2人选横店”为事件A,“从乙寝室选出的2人选横店”为事件B.
由于事件A、B相互独立,且P(A)=
=
,P(B)=
=
.…(4分)
所以选出的4人均选择横店的概率为
P(A•B)=P(A)•P(B)=
×
=
…(6分)
(Ⅱ)设ξ可能的取值为0,1,2,3.得
P(ξ=0)=
,
P(ξ=1)=
×
+
×
=
,
P(ξ=3)=
×
=
,
P(ξ=2)=1-P(ξ=0)-P(ξ=1)-P(ξ=3)=
…(12分)
ξ的分布列为
∴ξ的数学期望Eξ=0×
+1×
+2×
+3×
=1…(14分)
由于事件A、B相互独立,且P(A)=
| ||
|
| 2 |
| 3 |
| ||
|
| 2 |
| 5 |
所以选出的4人均选择横店的概率为
P(A•B)=P(A)•P(B)=
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
| 15 |
(Ⅱ)设ξ可能的取值为0,1,2,3.得
P(ξ=0)=
| 4 |
| 15 |
P(ξ=1)=
| ||
|
| ||||
|
| ||
|
| ||
|
| 22 |
| 45 |
P(ξ=3)=
| ||
|
| 1 | ||
|
| 1 |
| 45 |
P(ξ=2)=1-P(ξ=0)-P(ξ=1)-P(ξ=3)=
| 2 |
| 9 |
ξ的分布列为
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 4 |
| 15 |
| 22 |
| 45 |
| 2 |
| 9 |
| 1 |
| 45 |

练习册系列答案
相关题目
 为随机变量,求
为随机变量,求 的分布列为
的分布列为

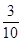

 ( )
( )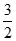 B.
B. C.
C.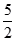 D.
D.
 :
:

 .
.