Question

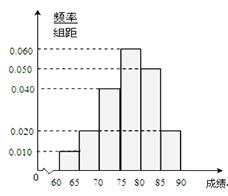
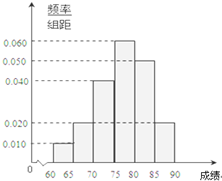在某次综合素质测试中，共设有40个考室，每个考室30名考生．在考试结束后，为调查其测试前的培训辅导情况与测试成绩的相关性，抽取每个考室中座位号为05的考生，统计了他们的成绩，得到如图所示的频率分布直方图．
（Ⅰ）在这个调查采样中，用到的是什么抽样方法？
（Ⅱ）写出这40个考生成绩的众数、中位数，平均数的估计值（只写结果）．

Answer 1

分析：（Ⅰ）先根据抽样方法的定义可知其为系统抽样；．
（II）选出直方图中最高的矩形，求出其底边的中点的横坐标即为众数；求出从左边开始小矩形的面积和为0.5对应的横轴的数值即为中位数；求各个小矩形的面积乘以对应矩形底边的中点之和即为平均数．

解答：解：（I）根据系统抽样方法的定义，∵是抽取每个考室中座位号为05的考生，
∴其为系统抽样；
（II）直方图中最高的矩形是成绩在[75，80]内的一组，∴众数是77.5；
从左边开始前三个小矩形的面积和为0.05+0.1+0.2=0.35，设中位数为75+x，
则0.3×x+0.35=0.5⇒x=5，∴中位数为80；
平均数为62.5×0.05+67.5×0.1+72.5×0.2+77.5×0.3+82.5×0.25+87.5×0.1=77.25．

点评：本题考查系统抽样方法及频率分布直方图特征数问题，利用众数是最高矩形底边中点的横坐标；中位数是左右两边矩形面积相等的底边的值；平均数是各个小矩形的面积×其底边中点值之和求解．