题目内容
证明:任何不大于n!的自然数,都能表示成不多于n个数的和,在这些加数中,没有两个是相同的,而且任何一个都是n!的因数.证明:对n用数学归纳法,
n=1时,显然.
设n时结论真.
对a≤(n+1)!,将a除以n+1得a=d(n+1)+r,这里d≤n!,0≤r<n+1.
由归纳假设,d=d1+d2+…+dl,l≤n.且所有di是n!的不同因数(i=1,2,…,l).
于是 a=d1(n+1)+…+dl(n+1)+r
这个和中的加数不多于n+1个,其中每一个都是(n+1)!的因数,且全不相等.

练习册系列答案
相关题目
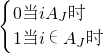 .
.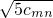 -
-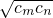 >1对任何正整数m,n都成立.(第1小题用表)
>1对任何正整数m,n都成立.(第1小题用表) .
.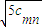 -
- >1对任何正整数m,n都成立.(第1小题用表)
>1对任何正整数m,n都成立.(第1小题用表)