题目内容
集合A1,A2,A3,…,An为集合M={1,2,3,…,n}的n个不同的子集,对于任意不大于n的正整数i,j满足下列条件:
①i∉Ai,且每一个Ai至少含有三个元素;
②i∈Aj的充要条件是j∉Aj(其中i≠j).
为了表示这些子集,作n行n列的数表(即n×n数表),规定第i行第j列数为:aij=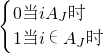 .
.
(1)该表中每一列至少有多少个1;若集合M={1,2,3,4,5,6,7},请完成下面7×7数表(填符合题意的一种即可);
(2)用含n的代数式表示n×n数表中1的个数f(n),并证明n≥7;
(3)设数列{an}前n项和为f(n),数列{cn}的通项公式为:cn=5an+1,证明不等式: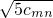 -
-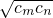 >1对任何正整数m,n都成立.(第1小题用表)
>1对任何正整数m,n都成立.(第1小题用表)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 0 | ||||||
| 2 | 0 | ||||||
| 3 | 0 | ||||||
| 4 | 0 | ||||||
| 5 | 0 | ||||||
| 6 | 0 | ||||||
| 7 | 0 |
解:(1)根据条件①每个Ai中至少含有三个元素,作出的数表每一列至少有三个1.7×7数表如下:
(2)题设条件①中的i∉Ai,表明的一条对角线上数字都是0,题设条件②表明除对角线以外,aij与aji恰好一个为1,
而另一个为0,即数表中除该对角线以外,0与1各占一半,故数表中共有f(n)= 个1.
个1.
另一方面,根据题设条件①每一个Ai至少含有三个元素得:
作出的n×n数表的每一列至少有3个1,所
以整个n×n数表(共有n列)至少有3n个1,
因此列出不等式: ≥3n,
≥3n,
解得n≥7.
(3)∵n≥2时,an=f(n)-f(n-1)=n-1
检验n=1也成立,故an=n-1
∴cn=5an+1=5n-4
要证: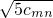 -
-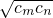 >1对任何正整数m,n都成立,
>1对任何正整数m,n都成立,
只要证:5cmn>1+cm•cn+
∵cmn=5mn-4,cm•cn=25mn-20(m+n)+16
故只要证:5(5mn-4)>1+25mn-20(m+n)+16+ ,
,
即只要证:20m+20n-37≥ ,又
,又
∵ ≤cm•cn=5m+5n-8<5m+5n-8+(15m+15n-29)=20m+20n-37
≤cm•cn=5m+5n-8<5m+5n-8+(15m+15n-29)=20m+20n-37
所以命题得证.
分析:(1)由已知中aij=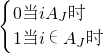 ,及①i∉Ai,且每一个Ai至少含有三个元素;②i∈Aj的充要条件是j∉Aj(其中i≠j).可得数据表中各个数据;
,及①i∉Ai,且每一个Ai至少含有三个元素;②i∈Aj的充要条件是j∉Aj(其中i≠j).可得数据表中各个数据;
(2)由条件①中的i∉Ai,表明的一条对角线上数字都是0,题设条件②表明除对角线以外,aij与aji恰好一个为1,可得数表中除该对角线以外,0与1各占一半,即 个1,而据题设条件①每一个Ai至少含有三个元素得:作出的n×n数表的每一列至少有3个1,所以整个n×n数表(共有n列)至少有3n个1,由此构造关于n的不等式,可求出n的范围
个1,而据题设条件①每一个Ai至少含有三个元素得:作出的n×n数表的每一列至少有3个1,所以整个n×n数表(共有n列)至少有3n个1,由此构造关于n的不等式,可求出n的范围
(3)由已知中确定出数列{an},数列{cn}的通项公式,可证得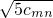 -
-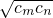 >1对任何正整数m,n都成立.
>1对任何正整数m,n都成立.
点评:本题考查的知识点是数列的应用,其中正确理解已知中条件:①i∉Ai,且每一个Ai至少含有三个元素;②i∈Aj的充要条件是j∉Aj(其中i≠j)的含义是解答本题的关键.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 2 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 3 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 4 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 6 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
而另一个为0,即数表中除该对角线以外,0与1各占一半,故数表中共有f(n)=
 个1.
个1.另一方面,根据题设条件①每一个Ai至少含有三个元素得:
作出的n×n数表的每一列至少有3个1,所
以整个n×n数表(共有n列)至少有3n个1,
因此列出不等式:
 ≥3n,
≥3n,解得n≥7.
(3)∵n≥2时,an=f(n)-f(n-1)=n-1
检验n=1也成立,故an=n-1
∴cn=5an+1=5n-4
要证:
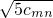 -
-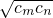 >1对任何正整数m,n都成立,
>1对任何正整数m,n都成立,只要证:5cmn>1+cm•cn+

∵cmn=5mn-4,cm•cn=25mn-20(m+n)+16
故只要证:5(5mn-4)>1+25mn-20(m+n)+16+
 ,
,即只要证:20m+20n-37≥
 ,又
,又∵
 ≤cm•cn=5m+5n-8<5m+5n-8+(15m+15n-29)=20m+20n-37
≤cm•cn=5m+5n-8<5m+5n-8+(15m+15n-29)=20m+20n-37所以命题得证.
分析:(1)由已知中aij=
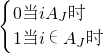 ,及①i∉Ai,且每一个Ai至少含有三个元素;②i∈Aj的充要条件是j∉Aj(其中i≠j).可得数据表中各个数据;
,及①i∉Ai,且每一个Ai至少含有三个元素;②i∈Aj的充要条件是j∉Aj(其中i≠j).可得数据表中各个数据;(2)由条件①中的i∉Ai,表明的一条对角线上数字都是0,题设条件②表明除对角线以外,aij与aji恰好一个为1,可得数表中除该对角线以外,0与1各占一半,即
 个1,而据题设条件①每一个Ai至少含有三个元素得:作出的n×n数表的每一列至少有3个1,所以整个n×n数表(共有n列)至少有3n个1,由此构造关于n的不等式,可求出n的范围
个1,而据题设条件①每一个Ai至少含有三个元素得:作出的n×n数表的每一列至少有3个1,所以整个n×n数表(共有n列)至少有3n个1,由此构造关于n的不等式,可求出n的范围(3)由已知中确定出数列{an},数列{cn}的通项公式,可证得
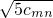 -
-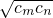 >1对任何正整数m,n都成立.
>1对任何正整数m,n都成立.点评:本题考查的知识点是数列的应用,其中正确理解已知中条件:①i∉Ai,且每一个Ai至少含有三个元素;②i∈Aj的充要条件是j∉Aj(其中i≠j)的含义是解答本题的关键.

练习册系列答案
相关题目
若A1,A2,…,Am为集合A={1,2,…,n}(n≥2且n∈N*)的子集,且满足两个条件:
①A1∪A2∪…∪Am=A;
②对任意的{x,y}⊆A,至少存在一个i∈{1,2,3,…,m},使Ai∩{x,y}={x}或{y}.则称集合组A1,A2,…,Am具有性质P.
如图,作n行m列数表,定义数表中的第k行第l列的数为akl=
.
(Ⅰ)当n=4时,判断下列两个集合组是否具有性质P,如果是请画出所对应的表格,如果不是请说明理由;
集合组1:A1={1,3},A2={2,3},A3={4};
集合组2:A1={2,3,4},A2={2,3},A3={1,4}.
(Ⅱ)当n=7时,若集合组A1,A2,A3具有性质P,请先画出所对应的7行3列的一个数表,再依此表格分别写出集合A1,A2,A3;
(Ⅲ)当n=100时,集合组A1,A2,…,At是具有性质P且所含集合个数最小的集合组,求t的值及|A1|+|A2|+…|At|的最小值.(其中|Ai|表示集合Ai所含元素的个数)
①A1∪A2∪…∪Am=A;
②对任意的{x,y}⊆A,至少存在一个i∈{1,2,3,…,m},使Ai∩{x,y}={x}或{y}.则称集合组A1,A2,…,Am具有性质P.
如图,作n行m列数表,定义数表中的第k行第l列的数为akl=
|
| a11 | a12 | … | a1m |
| a21 | a22 | … | a2m |
| … | … | … | … |
| an1 | an2 | … | anm |
集合组1:A1={1,3},A2={2,3},A3={4};
集合组2:A1={2,3,4},A2={2,3},A3={1,4}.
(Ⅱ)当n=7时,若集合组A1,A2,A3具有性质P,请先画出所对应的7行3列的一个数表,再依此表格分别写出集合A1,A2,A3;
(Ⅲ)当n=100时,集合组A1,A2,…,At是具有性质P且所含集合个数最小的集合组,求t的值及|A1|+|A2|+…|At|的最小值.(其中|Ai|表示集合Ai所含元素的个数)