题目内容
函数f(x)=-x2+(2a-1)|x|+1的定义域被分成了四个不同的单调区间,则实数a的取值范围是( )
A、a>
| ||||
B、
| ||||
C、a>
| ||||
D、a<
|
分析:先将f(x)=-x2+(2a-1)|x|+1看成是由函数f(x)=-x2+(2a-1)x+1变化得到,再将二次函数配方,找到其对称轴,明确单调性,再研究对称轴的位置即可求解.
解答: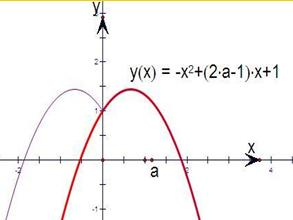 解:f(x)=-x2+(2a-1)|x|+1是由函数f(x)=-x2+(2a-1)x+1变化得到,
解:f(x)=-x2+(2a-1)|x|+1是由函数f(x)=-x2+(2a-1)x+1变化得到,
第一步保留y轴右侧的图象,再作关于y轴对称的图象.
因为定义域被分成四个单调区间,
所以f(x)=-x2+(2a-1)x+1的对称轴在y轴的右侧,使y轴右侧有两个单调区间,对称后有四个单调区间.
所以
>0,即a>
.
故选C
 解:f(x)=-x2+(2a-1)|x|+1是由函数f(x)=-x2+(2a-1)x+1变化得到,
解:f(x)=-x2+(2a-1)|x|+1是由函数f(x)=-x2+(2a-1)x+1变化得到,第一步保留y轴右侧的图象,再作关于y轴对称的图象.
因为定义域被分成四个单调区间,
所以f(x)=-x2+(2a-1)x+1的对称轴在y轴的右侧,使y轴右侧有两个单调区间,对称后有四个单调区间.
所以
| 2a-1 |
| 2 |
| 1 |
| 2 |
故选C
点评:本题主要考查二次函数配方法研究其单调性,同时说明单调性与对称轴和开口方向有关.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目