题目内容
16.已知函数f(x)=$\frac{{3{x^2}+ax}}{e^x}$(a∈R)在[4,+∞)上是减函数,则a的取值范围为( )| A. | (-∞,-8) | B. | (-8,0) | C. | (-8,8) | D. | (-8,+∞) |
分析 求函数的导数,利用函数单调性和导数之间的关系转化为在[4,+∞)上f′(x)≤0恒成立,利用换元法结合函数单调性的性质进行求解即可.
解答 解:函数的导数为f′(x)=$\frac{(6x+a){e}^{x}-(3{x}^{2}+ax){e}^{x}}{({e}^{x})^{2}}$=$\frac{6x+a-ax-3{x}^{2}}{{e}^{x}}$=$\frac{-3{x}^{2}+(6-a)x+a}{{e}^{x}}$,
若f(x)在[4,+∞)上是减函数,
则f′(x)≤0恒成立,
即-3x2+(6-a)x+a≤0,在[4,+∞)上恒成立,
即-3x2+6x+(1-x)a≤0[4,+∞)上恒成立,
即a≥$\frac{3{x}^{2}-6x}{1-x}$,
令x-1=t,则t≥3,且x=t+1,
则$\frac{3{x}^{2}-6x}{1-x}$=$\frac{3(t+1)^{2}-6(t+1)}{-t}$=$\frac{3{t}^{2}-3}{-t}$=-3t+$\frac{3}{t}$,
则函数y=3t+$\frac{3}{t}$则t≥3上为减函数,
∴-3t+$\frac{3}{t}$≤-3×3+1=-8,
则a≥-8,
故选:D.
点评 本题主要考查函数单调性的应用,求函数的导数,结合函数单调性和导数之间的关系,转化为不等式恒成立问题是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.在等差数列{an}中,若a1004+a1006+a1008=9,则该数列的前2011项的和为( )
| A. | 6033 | B. | 6030 | C. | 2011 | D. | 2010 |
1.若f(x)对于任意实数x恒有2f(x)-f(-x)=3x+1,则f(1)=( )
| A. | 2 | B. | 0 | C. | 1 | D. | -1 |
5.从点P(-1,2)引圆(x-1)2+(y+1)2=4的切线,则切线长是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
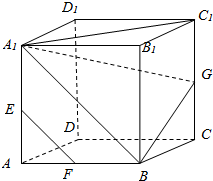 在正方体AC1中.
在正方体AC1中.