题目内容
7.双曲线S的中心在原点,焦点在x轴上,离心率e=$\frac{\sqrt{6}}{2}$,直线$\sqrt{3}$x-3y+5=0上的点与双曲线S的右焦点的距离的最小值等于$\frac{4\sqrt{3}}{3}$.(1)求双曲线S的方程;
(2)设经过点(-2,0),斜率等于k的直线与双曲线S交于A,B两点,且以A,B,P(0,1)为顶点的三角形ABP是以AB为底的等腰三角形,求k的值.
分析 (1)由离心率公式和点到直线的距离公式,结合a,b,c的关系,即可得到a,b,进而得到双曲线的方程;
(2)设直线AB:y=k(x+2),代入双曲线的方程,运用韦达定理,讨论k=0,k≠0,由中点坐标公式,结合两直线垂直的条件,可得k的方程,解方程即可得到k的值.
解答 解:(1)e=$\frac{c}{a}$=$\frac{\sqrt{6}}{2}$,又a2+b2=c2,
设右焦点为(c,0),由题意可得d=$\frac{|\sqrt{3}c+5|}{\sqrt{3+9}}$=$\frac{4\sqrt{3}}{3}$,
解得c=$\sqrt{3}$,b=1,a=$\sqrt{2}$,
可得双曲线的方程为$\frac{{x}^{2}}{2}$-y2=1;
(2)设直线AB:y=k(x+2),
当k=0时,可得A(-$\sqrt{2}$,0),B($\sqrt{2}$,0),
即有A,B,P(0,1)为顶点的三角形ABP
是以AB为底的等腰三角形;
当k≠0时,代入双曲线的方程可得
(1-2k2)x2-8k2x-8k2-2=0,
判别式△=64k4+4(1-2k2)(8k2+2)=8+16k2>0恒成立,
x1+x2=$\frac{8{k}^{2}}{1-2{k}^{2}}$,则AB的中点M坐标为($\frac{4{k}^{2}}{1-2{k}^{2}}$,$\frac{2k}{1-2{k}^{2}}$),
由题意可得PM⊥AB,可得kPM=-$\frac{1}{k}$,
即有$\frac{2k-1+2{k}^{2}}{4{k}^{2}}$=-$\frac{1}{k}$,解得k=$\frac{-3±\sqrt{11}}{2}$.
综上可得k=0,或k=$\frac{-3±\sqrt{11}}{2}$.
点评 本题考查双曲线的方程和性质,考查直线和双曲线的方程联立,运用韦达定理和中点坐标公式,以及两直线垂直的条件,属于中档题.

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案| A. | $\sqrt{2}$-1 | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\sqrt{3}$-1 |
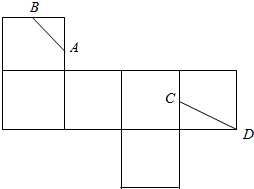 如图是一个正方体的平面展开图,A,B,C均为所在棱的中点,D为正方体的顶点,若正方体的棱长为2,则在正方体中,封闭折线ABCDA的长为3$\sqrt{2}+\sqrt{5}$.
如图是一个正方体的平面展开图,A,B,C均为所在棱的中点,D为正方体的顶点,若正方体的棱长为2,则在正方体中,封闭折线ABCDA的长为3$\sqrt{2}+\sqrt{5}$.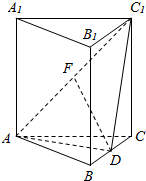 如图,在直三棱柱ABC-A1B1C1中,AB=AC,BD=DC,AF=C1F.
如图,在直三棱柱ABC-A1B1C1中,AB=AC,BD=DC,AF=C1F.