题目内容

点P（-3，1）在椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左准线上．过点P且方向为
a
=（2，-5）的光线，经直线y=-2反射后通过椭圆的左焦点，则这个椭圆的离心率为（　　）
A、
3
3
B、
1
3
C、
2
2
D、
1
2
分析：根据过点P且方向为a=（2，-5）求得PQ的斜率，进而可得直线PQ的方程，把y=2代入可求得Q的坐标，根据光线反射的对称性知直线QF1的斜率进而得直线QF1的方程，把y=0代入即可求得焦点坐标，求得c，根据点P（-3，1）在椭圆的左准线上，求得a和c的关系求得a，则椭圆的离心率可得．
解答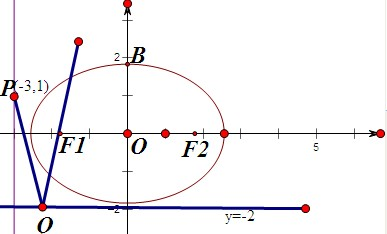：精英家教网解：如图，过点P（-3，1）的方向
a
=（2，-5）
所以KPQ=-
5
2
，则lPQ的方程为y-1=-
5
2
（x+3），
即LPQ=5x+2y=13与y=-2联立求得Q（-
9
5
，-2）
，由光线反射的对称性知：KQF1=
5
2

所以LQF1为y+2=
5
2
（x+
9
5
），
即5x-2y+5=0，
令y=0，得F1（-1，0），
综上所述得：c=1，
a2
c
=3，则a=
3
，
所以椭圆的离心率e=
c
a
=
3
3
，
故选A．
点评：本题主要考查了直线与椭圆的关系．充分利用了光线反射的性质．
练习册系列答案
相关题目
（2013•怀化三模）已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)过点(
3
，
3
2
)，离心率e=
1
2
，若点M（x0，y0）在椭圆C上，则点N(
x0
a
，
y0
b
)称为点M的一个“椭点”，直线l交椭圆C于A、B两点，若点A、B的“椭点”分别是P、Q，且以PQ为直径的圆经过坐标原点O．
（1）求椭圆C的方程；
（2）若椭圆C的右顶点为D，上顶点为E，试探究△OAB的面积与△ODE的面积的大小关系，并证明．
（2012•淮南二模）已知椭圆C：
x2
a2
+
y2
b2
=1，（a＞b＞0）与双曲4x2-
4
3
y2=1有相同的焦点，且椭C的离心e=
1
2
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．
（1）求椭圆的方程；
（2）若直MA交直x=4于点P，过P作直线MB的垂线x轴于点Q，Q的坐标；
（3）求点P在直线MB上射R的轨迹方程．
已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)过点(
3
，
3
2
)，离心率e=
1
2
，若点M（x0，y0）在椭圆C上，则点N(
x0
a
，
y0
b
)称为点M的一个“椭点”，直线l交椭圆C于A、B两点，若点A、B的“椭点”分别是P、Q，且以PQ为直径的圆经过坐标原点O．
（1）求椭圆C的方程；
（2）若椭圆C的右顶点为D，上顶点为E，试探究△OAB的面积与△ODE的面积的大小关系，并证明．
已知椭圆C：+=1，（a＞b＞0）与双曲4x2-y2=1有相同的焦点，且椭C的离心e=，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．
（1）求椭圆的方程；
（2）若直MA交直x=4于点P，过P作直线MB的垂线x轴于点Q，Q的坐标；
（3）求点P在直线MB上射R的轨迹方程．
已知椭圆C：+=1，（a＞b＞0）与双曲4x2-y2=1有相同的焦点，且椭C的离心e=，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．
（1）求椭圆的方程；
（2）若直MA交直x=4于点P，过P作直线MB的垂线x轴于点Q，Q的坐标；
（3）求点P在直线MB上射R的轨迹方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网