题目内容
某市举行一次数学新课程骨干培训活动,共邀请15名使用不同版本教材的数学教师,具体情况数据如下表所示:
现从这15名教师中随机选出2名,则2人恰好是教不同版本的女教师的概率是
.且a>b.
(1)求实数a,b的值
(2)培训活动现随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为ξ,求随机变量ξ的分布列和数学期望E(ξ).
| 版本 | 人教A版 | 人教B版 | ||
| 性别 | 男教师 | 女教师 | 男教师 | 女教师 |
| 人数 | 6 | a | 4 | b |
| 2 |
| 35 |
(1)求实数a,b的值
(2)培训活动现随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为ξ,求随机变量ξ的分布列和数学期望E(ξ).
分析:(1)由题意知本题是一个古典概型,试验发生包含的所有事件是从15个教师中选两个,而满足条件的事件是2人恰好是教不同版本的男教师,根据古典概型概率公式得到
=
,可解得ab=6,再结合a+b=5可得答案.
(2)培训活动随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为ξ,由题意知变量的可能取值是0,1,2,结合变量对应的事件和上一问,写出分布列和期望.
| ||||
|
| 2 |
| 35 |
(2)培训活动随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为ξ,由题意知变量的可能取值是0,1,2,结合变量对应的事件和上一问,写出分布列和期望.
解答:解:(1)从15名教师中随机选出2名共C
种选法,所以这2人恰好是教不同版本的女教师的概率是
=
.计算可得ab=6,
又∵a+b=5,且a>b,解得a=3,b=2
(2)由题意得ξ=0,1,2
P(ξ=0)=
=
;
P(ξ=1)=
=
;
故ξ的分布列为
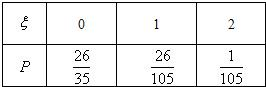
故数学期望E(ξ)=0×
+1×
+2×
=
2 15 |
| ||||
|
| 2 |
| 35 |
又∵a+b=5,且a>b,解得a=3,b=2
(2)由题意得ξ=0,1,2
P(ξ=0)=
| ||||
|
| 26 |
| 35 |
P(ξ=1)=
| ||||
|
| 26 |
| 105 |
故ξ的分布列为

故数学期望E(ξ)=0×
| 26 |
| 35 |
| 26 |
| 105 |
| 1 |
| 105 |
| 4 |
| 15 |
点评:求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题,题目做起来不难,运算量也不大,只要注意解题格式就问题不大.

练习册系列答案
相关题目
某市举行一次数学新课程骨干培训活动,共邀请15名使用不同版本教材的数学教师,具体情况数据如下表所示:
|
版本 |
人教A版 |
人教B版 |
||
|
性别 |
男教师 |
女教师 |
男教师 |
女教师 |
|
人数 |
6 |
|
4 |
|
现从这15名教师中随机选出2名,则2人恰好是教不同版本的女教师的概率是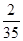 .且
.且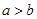 .
.
(1)求实数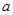 ,
,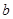 的值
的值
(2)培训活动现随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为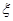 ,求随机变量
,求随机变量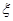 的分布列和数学期望
的分布列和数学期望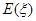 .
.
(本小题满分12分)
某市举行一次数学新课程骨干培训,共邀请15名使用不同版本教材的教师,数据如下表所示:
|
版本 |
人教A版 |
人教B版 |
||
|
性别 |
男教师 |
女教师 |
男教师 |
女教师 |
|
人数 |
6 |
3 |
4 |
2 |
(1)从这15名教师中随机选出2名,则2人恰好是教不同版本的男教师的概率是多少?
(2)培训活动随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为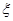 ,求随机变量
,求随机变量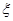 的分布列和数学期望
的分布列和数学期望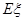 .
.
某市举行一次数学新课程骨干培训,共邀请15名使用不同版本教材的教师,数据如下表所示:
版本 | 人教A版 | 人教B版 | ||
性别 | 男教师 | 女教师 | 男教师 | 女教师 |
人数 | 6 | 3 | 4 | 2 |
(1)从这15名教师中随机选出2名,则2人恰好是教不同版本的男教师的概率是多少?
(2)培训活动随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(本小题满分12分)
某市举行一次数学新课程培训,共邀请15名研究不同版本教材的骨干教师,数据如下表所示:
| 版本 | 人教A版 | 人教B版 | ||
| 性别 | 男教师 | 女教师 | 男教师 | 女教师 |
| 人数 | 6 | 3 | 4 | 2 |
(Ⅰ)从这15名教师中随机选出2名,则2人恰好是研究不同版本教材的男教师的概率是多少?
(Ⅱ)培训活动随机选出2名代表发言,设发言代表中研究人教B版教材的女教师人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.