题目内容
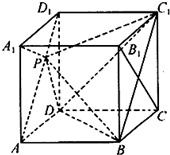 11、如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P在线段AD1上运动,给出以下四个命题:
11、如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P在线段AD1上运动,给出以下四个命题:①异面直线C1P与CB1所成的角为定值;
②二面角P-BC1-D的大小为定值;
③三棱锥D-BPC1的体积为定值;
④异面直线A1P与BC1间的距离为定值.
其中真命题的个数为( )
分析:对于①由题意及图形利用异面直线所成角的概念及求异面直线间的方法及可求解;
对于②由题意及平面具有延展性可知实质为平面ABC1D1与平面BDC1所成的二面角;
对于③由题意及三棱锥的体积的算法中可以进行顶点可以轮换性求解体积,和点P的位置及直线AD1与平面BDC1的位置即可判断正误;
对于④有异面直线间的距离的概念及这两个直线所在的平面的情况即可判断出答案.
对于②由题意及平面具有延展性可知实质为平面ABC1D1与平面BDC1所成的二面角;
对于③由题意及三棱锥的体积的算法中可以进行顶点可以轮换性求解体积,和点P的位置及直线AD1与平面BDC1的位置即可判断正误;
对于④有异面直线间的距离的概念及这两个直线所在的平面的情况即可判断出答案.
解答:解:对于①因为在棱长为1的正方体ABCD-A1B1C1D1中,点P在线段AD1上运动,有正方体的及题意易有B1C⊥平面ABC1D1,而C1P?平面ABC1D1,所以B1C⊥C1P,故这两个异面直线所成的角为定值90°,所以①正确;
对于②因为二面角P-BC1-D的大小,实质为平面ABC1D1与平面BDC1所成的二面角而这两的平面为固定的不变的平面所以夹角也为定值,故②正确;
对于③三棱锥D-BPC1的体积还等于三棱锥的体积P-DBC1的体积,而平面DBC1为固定平面且大小一定,又因为P∈AD1,
而AD1∥平面BDC1,所以点A到平面DBC1的距离即为点P到该平面的距离,所以三棱锥的体积为定值,故③正确;
对于④由意面直线间的距离定义及求法,因为直线A1P和BC1分别位于平面ADD1A1和
平面BCC1B1中,且这两个平面平行,故这两个平面间的距离即为所求的异面直线间的距离,所以这两个异面直线间的距离为定值,故④正确;
故选D
对于②因为二面角P-BC1-D的大小,实质为平面ABC1D1与平面BDC1所成的二面角而这两的平面为固定的不变的平面所以夹角也为定值,故②正确;
对于③三棱锥D-BPC1的体积还等于三棱锥的体积P-DBC1的体积,而平面DBC1为固定平面且大小一定,又因为P∈AD1,
而AD1∥平面BDC1,所以点A到平面DBC1的距离即为点P到该平面的距离,所以三棱锥的体积为定值,故③正确;
对于④由意面直线间的距离定义及求法,因为直线A1P和BC1分别位于平面ADD1A1和
平面BCC1B1中,且这两个平面平行,故这两个平面间的距离即为所求的异面直线间的距离,所以这两个异面直线间的距离为定值,故④正确;
故选D
点评:对于①重点考查了异面直线所成角的概念及求异面直线间的方法;
对于②重点考查了平面具有延展性及二面角的求法及其定义;
对于③重点考查了三棱锥的体积的体积计算可以进行顶点轮换及线面平行时,直线上任意一点到平面的距离都行等这一结论;
对于④重点考查了异面直线间的距离概念及这两个直线所在的平面平行时两平面间的距离即为异面直线间的距离这一结论.
对于②重点考查了平面具有延展性及二面角的求法及其定义;
对于③重点考查了三棱锥的体积的体积计算可以进行顶点轮换及线面平行时,直线上任意一点到平面的距离都行等这一结论;
对于④重点考查了异面直线间的距离概念及这两个直线所在的平面平行时两平面间的距离即为异面直线间的距离这一结论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
