题目内容
如图所示，已知矩形ABCD中，AB＝1，BC＝a(a＞0)，PA⊥面ABCD．
(1)问BC边上是否存在点Q，使得PQ⊥QD，并说明理由．
(2)若PA＝1，且BC边上有且只有一点Q，使得PQ⊥QD．求这时二面角Q－PD－A的大小．
答案：
解析：
解析：
|
(1)当a＝2时，BC边上有中点，满足PQ⊥QD．当0＜a＜2时，BC边上不存在点Q，满足PQ⊥QO． (2)所求二面角Q－PD－A的大小为arctan |
练习册系列答案
相关题目
，
)．
|；若不存在，请说明理由．
＋
＝1(a＞b＞0)，A，P，F分别为左顶点，上顶点，右焦点，E为x轴正方向上一点，且|
|，|
|，|
|成等比数列．又点N满足
＝
(
＋
)，PF的延长线与椭圆的交点为Q，过Q与x轴平行的直线与PN的延长线交于M．
·
＝
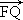，且|
，求椭圆方程．
，现在发现电路不通了，那么至少有两个焊接点脱落的概率是多少？
，|BC|＝2|AC|．
．