题目内容
14.已知数列{an}中,an=1+$\frac{1}{a+2(n-1)}$(n∈N*,a∈R,且a≠0)若对任意的n∈N*.都有an≤a6成立,求a的取值范围.分析 通过记f(x)=1+$\frac{1}{2[x-(1-\frac{a}{2})]}$可知其图象关于点(1-$\frac{a}{2}$,1)成中心对称,利用a6为最大项计算即得结论.
解答 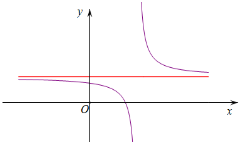 解:记f(x)=1+$\frac{1}{a+2(x-1)}$=1+$\frac{1}{2[x-(1-\frac{a}{2})]}$,
解:记f(x)=1+$\frac{1}{a+2(x-1)}$=1+$\frac{1}{2[x-(1-\frac{a}{2})]}$,
则函数f(x)的图象关于点(1-$\frac{a}{2}$,1)成中心对称,
且在区间(-∞,1-$\frac{a}{2}$)、(1-$\frac{a}{2}$,+∞)上均单调递减,
依题意,a6为最大项,
∴5<1-$\frac{a}{2}$<6,
解得:-10<a<-8.
点评 本题以数列为载体,考查函数的单调性,注意解题方法的积累,属于中档题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目