题目内容
下列关于实数x的不等关系中,恒成立的是
- A.|x-1|-|x+2|≤3
- B.x+
 ≥2
≥2 - C.
 +
+ ≤1
≤1 - D.x2+1>2x
A
分析:|x-1|-|x+2|≤3,的解集是R故A恒成立;x+ ≥2的前提条件是x>0,当x≤0时,B不成立;当
≥2的前提条件是x>0,当x≤0时,B不成立;当 时,
时, +
+ =
= >1,故
>1,故 +
+ ≤1不恒立;当x=1时,x2+1=2x,故x2+1>2x不恒成立.
≤1不恒立;当x=1时,x2+1=2x,故x2+1>2x不恒成立.
解答:在A中,|x-1|-|x+2|≤3,
由x-1=0,得x=1;由x+2=0,得x=-2.
①当x≥1时,x-1-x-2=-3≤3,成立,
∴x≥1;
②当-2≤x<1时,1-x-x-2=-1≤3,成立,
∴-2≤x<1;
③当x<-2时,1-x+x+2=3≤3,成立,
∴x<-2.
综上所述,x∈R.
故A恒成立;
在B中,x+ ≥2的前提条件是x>0,
≥2的前提条件是x>0,
当x≤0时,B不成立;
在C中,当 时,
时, +
+ =
= >1,
>1,
故 +
+ ≤1不恒立;
≤1不恒立;
在D中,当x=1时,x2+1=2x,
故x2+1>2x不恒成立.
故选A.
点评:本题考查函数的恒成立问题,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.
分析:|x-1|-|x+2|≤3,的解集是R故A恒成立;x+
 ≥2的前提条件是x>0,当x≤0时,B不成立;当
≥2的前提条件是x>0,当x≤0时,B不成立;当 时,
时, +
+ =
= >1,故
>1,故 +
+ ≤1不恒立;当x=1时,x2+1=2x,故x2+1>2x不恒成立.
≤1不恒立;当x=1时,x2+1=2x,故x2+1>2x不恒成立.解答:在A中,|x-1|-|x+2|≤3,
由x-1=0,得x=1;由x+2=0,得x=-2.
①当x≥1时,x-1-x-2=-3≤3,成立,
∴x≥1;
②当-2≤x<1时,1-x-x-2=-1≤3,成立,
∴-2≤x<1;
③当x<-2时,1-x+x+2=3≤3,成立,
∴x<-2.
综上所述,x∈R.
故A恒成立;
在B中,x+
 ≥2的前提条件是x>0,
≥2的前提条件是x>0,当x≤0时,B不成立;
在C中,当
 时,
时, +
+ =
= >1,
>1,故
 +
+ ≤1不恒立;
≤1不恒立;在D中,当x=1时,x2+1=2x,
故x2+1>2x不恒成立.
故选A.
点评:本题考查函数的恒成立问题,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
下列关于实数x的不等关系中,恒成立的是( )
A、x+
| ||||
| B、x2+1>2x | ||||
C、
| ||||
| D、|x-1|-|x+2|≤3 |
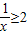
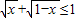
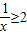
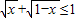
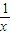 ≥2
≥2 +
+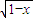 ≤1
≤1