题目内容

11．如图，在△ABC中，D在AB上，E在AC的延长线上，BD=CE，连接DE，交BC于F，∠BAC外角的平分线交BC的延长线于G，且AG∥DE．求证：BF=CF．

分析 利用∠BAC外角的平分线交BC的延长线于G，AG∥DE，可得∠ADE=∠AED，过点C作CM∥AB交DE于M，证明四边形BMCD为平行四边形，即可得出结论．

解答 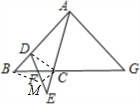证明：因为∠BAC外角的平分线交BC的延长线于G，AG∥DE，
所以，∠ADE=∠AED；
过点C作CM∥AB交DE于M，所以，CM=CE=BD，
所以，四边形BMCD为平行四边形，所以，BF=CF．

点评 本题考查三角形外角平分线的性质，考查平行四边形的证明，比较基础．

练习册系列答案
相关题目
1．四棱锥S-ABCD的底面ABCD是正方形，AC与BD相交于点O，且SO⊥平面ABCD，若四棱锥S-ABCD的体积为12，底面对角线的长为2$\sqrt{8}$，则侧面与底面所成的二面角等于60°．
2．已知数列a-1，a2-2，a3-3…an-n，求Sn．
19．函数y=logsinx（2cosx+1）的定义域为{x|2kπ＜x＜2kπ+$\frac{2π}{3}$，且x≠2kπ+$\frac{π}{2}$，k∈Z}．
6．已知在△ABC中，a=5，c=7，sinA=$\frac{5\sqrt{3}}{14}$，则∠C=60°或120°．
16．在直角坐标系xOy中，极点与原点重合，极轴与x轴正半轴重合，已知圆C的参数方程为$\left\{\begin{array}{l}{x=cosα}\\{y=1+sinα}\end{array}\right.$（α为参数，α∈R），则此圆圆心的极坐标为$（1，\frac{π}{2}）$．
3．如图：正三棱柱ABC-A1B1C1中，D是BC的中点，AA1=AB=1．
（1）求证：A1C∥平面AB1D；
（2）求点C到平面AB1D的距离．
（3）求二面角B-AB1-D的大小．
20．圆心在（1，-2），半径为2$\sqrt{5}$的圆在x轴上截得的弦长等于（　　）
A．4$\sqrt{3}$B．6C．6$\sqrt{2}$D．8
1．设a=log32，b=ln2，c=0.5-0.1，则（　　）
A．a＜b＜cB．b＜a＜cC．c＜a＜bD．c＜b＜a

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网