题目内容
(任选一题)(1)已知α、β为实数,给出下列三个论断:
①|α-β|≤|α+β|②|α+β|>5 ③|α|>2
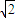 ,|β|>2
,|β|>2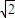
以其中的两个论断为条件,另一个论断为结论,写出你认为正确的命题是 .
(2)设{an}和{bn}都是公差不为零的等差数列,且
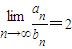 ,则
,则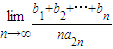 的值为 .
的值为 .
【答案】分析:(1)观察知,可由①③推出②,本题是一个开放式题,结论可能不唯一,本题只证明①③推出②,首先由①|α-β|≤|α+β|得出α与β同号,再结合③得出|α+β|的取值范围,与5比较即可得到结论.
(2)设{an}和{bn}的公差分别为d1 和d2,有条件可得d1=2d2,根据等差数列的通项公式及前n项和公式化简要求的式子
并把d1=2d2代入,再利用数列极限的运算法则求出结果.
解答:(1)解:由①|α-β|≤|α+β|知,α,β同号,故|α+β|=|α|+|β|,
又由③|α|>2 ,|β|>2
,|β|>2  可得|α+β|>4
可得|α+β|>4  ,
,
又4 ≈5.6>5,
≈5.6>5,
所以有|α+β|>5成立,
综上知①③推出②,
故答案为①③⇒②.
(2)解:设{an}和{bn}的公差分别为d1 和d2,
∵ =
=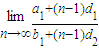 =
= =2,∴d1=2d2.
=2,∴d1=2d2.
 =
= =
= =
= =
= ,
,
故答案为: .
.
点评:第(1)题考察不等式的证明,解题的关键是判断出条件与结论,本题难点是判断出那两个做条件可以保证第三个成立,此类题是开放式题答案可能不唯一,故找出一个正确的来就行,此类题开放式题在近几年新教材实验区基本上不出现了,本题较抽象,不易想,容易出错.
第(2)题主要考查等差数列的通项公式,前n项和公式,求数列的极限的方法,得到d1=2d2,是解题的关键.
(2)设{an}和{bn}的公差分别为d1 和d2,有条件可得d1=2d2,根据等差数列的通项公式及前n项和公式化简要求的式子
并把d1=2d2代入,再利用数列极限的运算法则求出结果.
解答:(1)解:由①|α-β|≤|α+β|知,α,β同号,故|α+β|=|α|+|β|,
又由③|α|>2
 ,|β|>2
,|β|>2  可得|α+β|>4
可得|α+β|>4  ,
,又4
 ≈5.6>5,
≈5.6>5,所以有|α+β|>5成立,
综上知①③推出②,
故答案为①③⇒②.
(2)解:设{an}和{bn}的公差分别为d1 和d2,
∵
 =
=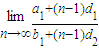 =
= =2,∴d1=2d2.
=2,∴d1=2d2. =
= =
= =
= =
= ,
,故答案为:
 .
.点评:第(1)题考察不等式的证明,解题的关键是判断出条件与结论,本题难点是判断出那两个做条件可以保证第三个成立,此类题是开放式题答案可能不唯一,故找出一个正确的来就行,此类题开放式题在近几年新教材实验区基本上不出现了,本题较抽象,不易想,容易出错.
第(2)题主要考查等差数列的通项公式,前n项和公式,求数列的极限的方法,得到d1=2d2,是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)