题目内容
已知函数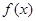 对任意
对任意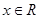 都有
都有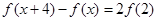 ,若
,若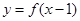 的图象关于直线
的图象关于直线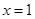 对称,且
对称,且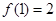 ,则
,则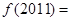
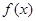 对任意
对任意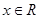 都有
都有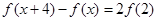 ,若
,若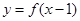 的图象关于直线
的图象关于直线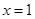 对称,且
对称,且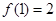 ,则
,则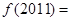
| A.2 | B.3 | C.4 | D.6 |
A
分析:先由函数f(x-1)的图象关于直线x=1对称,得函数f(x)的图象关于直线x=0对称,即函数f(x)是偶函数,故有f(-x)=f(x).再把-2代入f(x+4)-f(x)=2f(2),可得函数周期为4;就把f(2011)转化为f(3)=f(-1)=f(1)即可求解.
解:∵函数f(x-1)的图象关于直线x=1对称,
∴函数f(x)的图象关于直线x=0对称,即函数f(x)是偶函数,
∴f(-x)=f(x).
∵对任意x∈R,都有f(x+4)-f(x)=2f(2),
∴f(-2+4)=f(-2)+2f(2)
∴f(-2)+f(2)=0,
即2f(2)=0,
∴f(2)=0.
∴f(x+4)=f(x)+2f(2)=f(x),即函数周期为4.
∴f(2011)=f(4×502+3)=f(3)=f(-1)=f(1)=2.
故选A.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
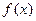 对任意的
对任意的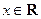 ,均有
,均有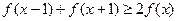 ,则称函数
,则称函数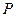 .
.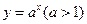 ; ②
; ②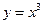 .
.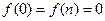 (
(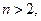
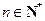 ),
),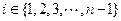 有
有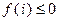 ;
;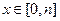 均有
均有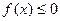 .若成立给出证明,若不成立给出反例.
.若成立给出证明,若不成立给出反例.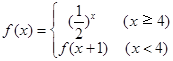 ,则
,则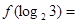




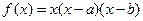 ,其中
,其中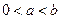 ,
,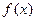 在
在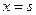 及
及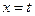 处取得极值,其中
处取得极值,其中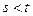 .
.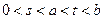 ;
;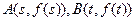 的中点
的中点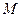 在曲线
在曲线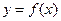 上.
上.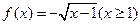 的反函数是 .
的反函数是 .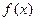 的定义域为
的定义域为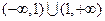 ,且
,且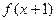 为奇函数,当
为奇函数,当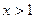 时,
时, 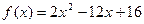 ,则直线
,则直线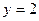 与函数
与函数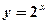 与
与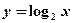 的图像关于直线
的图像关于直线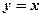 对称;②为了得到函数
对称;②为了得到函数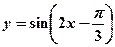 的图象,只需把函数
的图象,只需把函数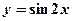 的图象上的所有点向右平移
的图象上的所有点向右平移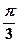 个单位长度; ③当
个单位长度; ③当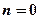 或
或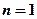 时,
时, 幂函数
幂函数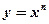 的图象都是一条直线;④已知函数
的图象都是一条直线;④已知函数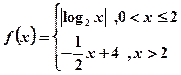 ,
, 若
若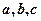 互不相等,且
互不相等,且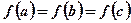 ,则
,则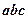 的取值
的取值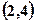 .
. 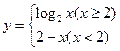 ,右下图表示的是给定
,右下图表示的是给定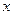 的值,求其
的值,求其 对应的函数值
对应的函数值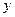 的程序框图,①处应填写 ;
的程序框图,①处应填写 ; 应填写 。
应填写 。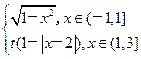 其中t>0.若函数y=
其中t>0.若函数y=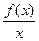 -
-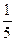 的零点个数是5,则t的取值范
的零点个数是5,则t的取值范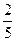 ,1)
,1)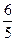 )
)