题目内容
5.高中某班语文、数学、英语、物理、化学、体育六门课安排在某一天,每门课程一节,上午四节,下午两节,若数学课必须在上午,体育课必须在下午,数、理、化三门课中,任何两门课不相邻(上午第四节与下午第一节不叫相邻),则课程安排的种数为( )| A. | 24 | B. | 96 | C. | 48 | D. | 124 |
分析 由题意可知,物理与化学只有一门可以排在下午(不妨用a代替),先研究上午的四节课,数学应与之间隔一节或间隔两节.再研究下午的情况,利用乘法原理即可得出结论.
解答 解:由题意可知,物理与化学只有一门可以排在下午(不妨用a代替),
先研究上午的四节课,数学应与之间隔一节或间隔两节.
间隔一节时,把数学、语文(或外语)、a(物理或化学)看成一个大元素,先选后排,攘外后安内的方式,共有${C}_{2}^{1}$•${C}_{2}^{1}$•${A}_{2}^{2}$•${A}_{2}^{2}$=16种(方法);
间隔两节时,共有${C}_{2}^{1}$•${A}_{2}^{2}$•${A}_{2}^{2}$=8种(方法);
故上午共有16+8=24种(方法).
再研究下午的情况,下午,体育有2种方法,其余排上午剩下的物理或化学,
利用乘法原理可得24×2=48种.
故选:C.
点评 本题考查分步计数原理,考查排列组合的实际应用,正确分步是关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
15.在△ABC中,已知∠A:∠B=1:2,角C的平分线CD把三角形面积分为4:3两部分,则cosA=( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
16.函数f(x)=sin2x+sin(2x+$\frac{π}{3}$)+sin(2x-$\frac{π}{3}$)的最小正周期为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
17.若正项数列{an}中,a1+a2+a3+…+an=$\frac{1}{2}$(an+$\frac{1}{{a}_{n}}$),n∈N*.则数列{an}的通项公式为( )
| A. | an=$\sqrt{n}$-$\sqrt{n-1}$ | B. | an=$\sqrt{n}$+$\sqrt{n-1}$ | C. | an=$\sqrt{n}$-$\sqrt{n+1}$ | D. | an=$\sqrt{n}$+$\sqrt{n+1}$ |
15.若sin(π-α)=log8$\frac{1}{4}$,则cos(π+α)的值为( )
| A. | $\frac{\sqrt{5}}{3}$ | B. | -$\frac{\sqrt{5}}{3}$ | C. | ±$\frac{\sqrt{5}}{3}$ | D. | 以上都不对 |
 已知△ABC满足∠B>∠C,∠A的平分线和过顶点的高线、中线与边BC分别交与点L、H、D.证明∠HAL=∠DAL的充分必要条件是∠BAC=90°.
已知△ABC满足∠B>∠C,∠A的平分线和过顶点的高线、中线与边BC分别交与点L、H、D.证明∠HAL=∠DAL的充分必要条件是∠BAC=90°.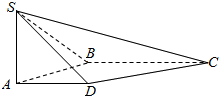 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2.
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2.