题目内容
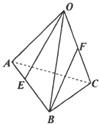 如图,已知四面体O-ABC中,E、F分别为AB,OC上的点,且AE=
如图,已知四面体O-ABC中,E、F分别为AB,OC上的点,且AE=| 1 | 3 |
分析:本题可利用向量运算来解答,设空间一组基底
,
,
,利用空间向量基本定理表示出向量
,
,可利用向量的数量积以及夹角公式解得向量
,
的夹角余弦值cos<
,
>,从而得到异面直线的夹角余弦值|cos<
,
>|.
| BO |
| BC |
| BA |
| BF |
| OE |
| BF |
| OE |
| BF |
| OE |
| BF |
| OE |
解答:解:∵
=
(
+
),
=
-
,
∴|
|2=
(|
|2+|
|2+2
•
)=
(4+1+2|
||
|cos60°)=
,|
|=
;|
|2=
|
|2+|
|2-
•
=4+4-4=4,|
|=2.
又
•
=
(
•
-|
|2+
•
-
•
)=
(2-4-1)=-
,
∴cos<
,
>=
=
=-
,
故异面直线OE与BF所成的角的余弦值为:
.
| BF |
| 1 |
| 2 |
| BO |
| BC |
| OE |
| 2 |
| 3 |
| BA |
| BO |
∴|
| BF |
| 1 |
| 4 |
| BO |
| BC |
| BO |
| BC |
| 1 |
| 4 |
| BO |
| BC |
| 7 |
| 4 |
| BF |
| ||
| 2 |
| OE |
| 4 |
| 9 |
| BA |
| BO |
| 4 |
| 3 |
| BA |
| BO |
| OE |
又
| BF |
| OE |
| 1 |
| 2 |
| 2 |
| 3 |
| BA |
| BO |
| BO |
| 2 |
| 3 |
| BC |
| BA |
| BC |
| BO |
| 1 |
| 2 |
| 3 |
| 2 |
∴cos<
| BF |
| OE |
| ||||
|
|
| -3 | ||
2
|
3
| ||
| 14 |
故异面直线OE与BF所成的角的余弦值为:
3
| ||
| 14 |
点评:本题考查空间几何体的概念,异面直线以及异面直线所成角的概念,向量法解答几何问题的“三步曲”思想的应用,考查了向量的数量积的运算律,夹角公式,空间向量基本定理的应用.

练习册系列答案
相关题目



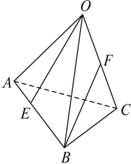
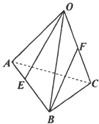 如图,已知四面体O-ABC中,E、F分别为AB,OC上的点,且AE=
如图,已知四面体O-ABC中,E、F分别为AB,OC上的点,且AE= AB,F为中点,若AB=3,BC=1,BO=2,且∠ABC=90°,∠OBA=∠OBC=60°,求异面直线OE与BF所成角的余弦值.
AB,F为中点,若AB=3,BC=1,BO=2,且∠ABC=90°,∠OBA=∠OBC=60°,求异面直线OE与BF所成角的余弦值.